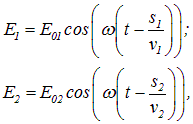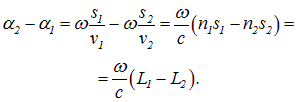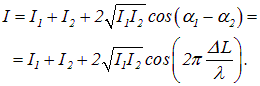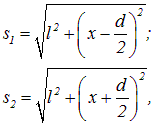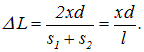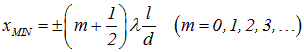4.3. Интерференция света от двух источников

Механизм излучения электромагнитных волн заключается в том, что атом, находящийся в возбужденном состоянии, при переходе на более низкий энергетический уровень излучает электромагнитную волну. Процесс излучения длится около  с. Таким образом, атом излучает волну, представляющую собой часть синусоиды (см. рис. 4.2), которая называется волновым цугом.

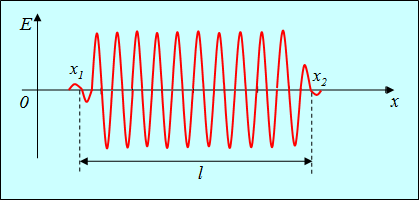
Рис. 4.2. Волновой цуг

Длина волнового цуга в вакууме равна

Естественный свет представляется совокупностью несогласованных между собой цугов волн, испускаемых отдельными атомами. Поэтому невозможно получить интерференцию от двух разных источников естественного света. Для получения когерентных световых волн тем или иным способом разделяют на две части волну, излучаемую одним источником. После прохождения различных оптических путей эти две части одной волны накладываются друг на друга (рис. 4.3).

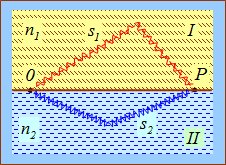
Рис. 4.3. Разделение волны от естественного источника

Предположим, что разделение на две когерентные волны происходит в некоторой точке 0, лежащей на границе раздела двух сред I и II. До точки Р в которой наблюдается интерференционная картина, одна волна проходит путь s₁ в среде с показателем преломления п₁, а вторая волна — путь s₂ в среде с показателем преломления п₂. Если начальные фазы обеих волн равны нулю, то в точке Р волны возбудят колебания

где

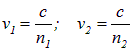
— фазовые скорости первой и второй волн соответственно. Разность фаз колебаний в точке Р равна

Выражая циклическую частоту через длину волны l в вакууме

находим

 

Запишем интенсивность результирующей волны в точке Р в виде

Когда оптическая разность хода равна целому числу длин волн в вакууме (или, что то же самое, четному числу полуволн), то есть

колебания в точке Р находятся в одинаковой фазе,  и наблюдается интерференционный максимум.

Если оптическая разность хода равна нечетному числу полуволн, то есть

то колебания, возбуждаемые в точке Р обеими волнами, находятся в противофазе,  и наблюдается интерференционный минимум.

Установив общие закономерности, обратимся к конкретному примеру интерференции, когда источниками света служат две узкие параллельные щели, расположенные достаточно близко друг к другу. Пусть эти щели S₁, и S₂ находятся на расстоянии d друг от друга (рис. 4.4).

Рис. 4.4. Интерференция от двух когерентных источников света

Интерференция наблюдается в некоторой точке Р экрана, расположенного на расстоянии l от источников света (l>>d, ). Начало отсчета на оси 0х выбрано в точке 0, симметричной относительно щелей.

Интенсивность в точке Р, расположенной на расстоянии x от начала отсчета, определяется оптической разностью хода, которая в данном случае (п = 1) равна геометрической разности хода

Видно, что

откуда

или

Учитывая, что при l>>d

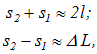
получаем

Используя условия (4.14) и (4.15) для максимумов и минимумов интерференции, приходим к выводу, что в точках с координатами

будут наблюдаться максимумы, а в точках

— интерференционные минимумы.

С учетом (4.20) ширина интерференционной полосы равна

причем  не зависит от порядка интерференции (величины т) и является постоянной величиной при заданных l, d, .

Видео 4.5 Интерферометр Маха-Цандера. Поворот стеклянной пластинки.

Видео 4.6 Интерферометр Маха-Цандера. «Деформация» основания.