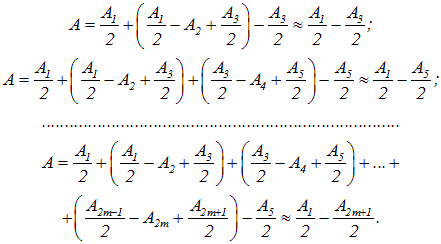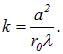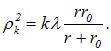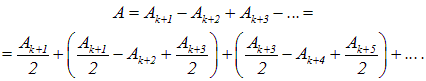5.3. Дифракция на круглом отверстии и диске
Схожие дифракционные явления можно наблюдать при прохождении света через малое отверстие или, как принято говорить, от дополнительного экрана — диска, размером в это отверстие. Пусть плоская световая волна падает на малое круглое отверстие радиусом а (рис. 5.3).
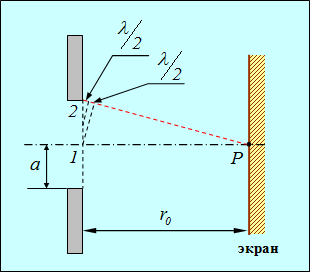
Рис. 5.3. Дифракция света на круглом отверстии
Плоский фронт, совпадающий с отверстием, можно рассматривать как совокупность фиктивных источников, испускающих когерентные волны, которые в точке наблюдения Р будут интерферировать. Разобьем площадь отверстия на ряд кольцевых зон Френеля, для чего из точки Р проведем ряд сфер с радиусами:
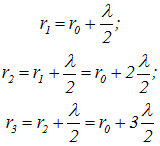
и т. д.
Если число зон, которые укладываются в отверстии, четно, то в точке Р будет темное пятно. Действительно, результирующая амплитуда колебаний при 2-х, 4-х, ... 2m зонах равна соответственно
|
|
|
(5.13) |
При небольших отверстиях (небольших m) амплитуды А1 и Аm2+1 мало отличаются друг от друга, поэтому результирующая амплитуда будет мала, и в точке наблюдения будет темное пятно.
При нечетном числе зон k = 2m-1 (m=1, 2, 3, ...) аналогичные рассуждения приводят к выражению
|
|
|
(5.14) |
то есть в точке наблюдения будет светлое пятно.
Число зон Френеля, укладывающихся в отверстии, зависит от расстояния 
и длины волны 
:
|
|
|
(5.15) |
откуда число открытых зон получается равным
|
|
|
(5.16) |
Таким образом, при данном радиусе отверстия а и длине волны падающего света 
число зон Френеля к является функцией расстояния 
между отверстием и точкой наблюдения.
Расчет амплитуды результирующих колебаний, пришедших в другие точки экрана, более сложен. Из соображений симметрии следует, что интерференционная картина на экране вокруг центрального светлого (или темного) пятна (в зависимости от четности числа k) должна иметь вид чередующихся светлых и темных колец с центрами в точке Р. Интенсивность максимумов должна убывать при удалении от точки Р.
Если источник света расположен перед отверстием на конечном расстоянии r до него, то расчет зон Френеля слегка усложняется: зоны проводятся не на плоском, а на сферическом фронте. Приведем без вывода выражение для радиусов зон Френеля в этом случае:
|
|
|
(5.17) |
При
приходим к формуле (5.4) для плоской волны.
Видео 5.5 Круглое отверстие. Переход от геометрической оптики к дифракции Френеля.
Видео 5.6 Круглое отверстие. Переход от дифракции Френеля к дифракции Фраунгофера.
Поместим теперь между падающей плоской волной и точкой наблюдения Р непрозрачный диск того же радиусом а — дополнительный экран (рис. 5.4).
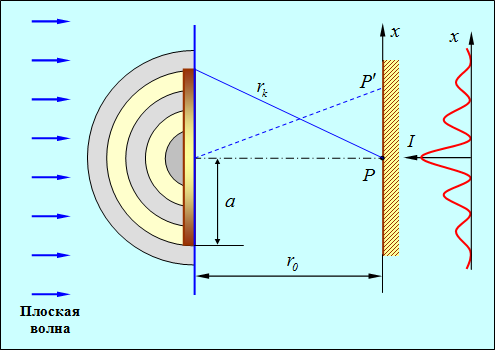
Рис. 5.4. Дифракция света на непрозрачном диске: справа показано распределение освещенности экрана в зависимости от расстояния х от центра экрана.
Светлое пятно в центре (максимальное значение интенсивности света I) сменяется чередующимися минимумами и максимумами, образующими светлые и темные кольца
Если диск закроет k первых зон Френеля, то амплитуда в точке Р будет равна
|
|
|
(5.18) |
Выражения в скобках, как и в формуле (5.13), можно положить равными нулю, то есть
|
|
|
(5.19) |
Таким образом, за небольшим непрозрачным диском
в центре экрана будет светлое пятно. Чем больше диск, тем, очевидно, амплитуда Аk+1 меньше, и освещенность пятна слабее, то есть дифракция менее существенна. Для точки Р', смещенной относительно точки Р в любом радиальном направлении, диск будет перекрывать часть (k + 1)-й зоны Френеля, одновременно откроется часть зоны k. Это вызовет уменьшение интенсивности. При некотором положении точки Р' интенсивность достигает минимума. Следовательно, в случае непрозрачного круглого диска дифракционная картина имеет вид светлого центрального пятна и чередующихся темных и светлых концентрических колец (см. рис. 5.4). Светлое пятно в центре геометрической тени, предсказанное С. Пуассоном в 1818 г., выдвигалось в качестве опровержения волновой теории света. Однако Д. Араго на опыте доказал, что выводы Пуассона соответствуют действительности и лишь подтверждают волновую теорию и ее предсказания, вытекающие из метода зон Френеля.
Видео 5.8 Пятно Пуассона (видимый свет).
Видео 5.9 Пятно Пуассона (трехсантиметровые волны).
Пример 1. На диафрагму с круглым отверстием диаметром d = 4 мм падает по нормали плоская волна света (
мкм). Точка наблюдения находится на расстоянии b = 1 м на оси отверстия. Определим, сколько зон Френеля укладывается в отверстии.
Используем (5.16) при а = d/2 и r0 = b:
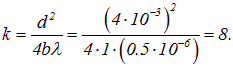
В центре картины будет темное пятно.
Пример 2. Точечный источник света ( мкм) расположен на расстоянии l = 1 м на оси диафрагмы с отверстием радиусом а = 1 мм. За отверстием помещают экран. Найдем, при каком расстоянии от отверстия до экрана для центра дифракционной картины будут открыты 3 зоны Френеля.
Используем формулу (5.17):
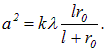
Отсюда находим
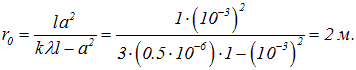
В центре дифракционной картины при k = 3 будет светлое пятно, и в соответствии с формулой (5.14) амплитуда колебаний в этой точке будет равна
Если диафрагму убрать, то амплитуда станет равной A1/2, то есть освещенность (интенсивность света) уменьшится в четыре раза.
