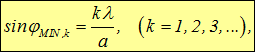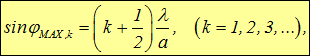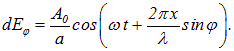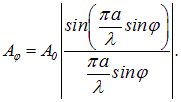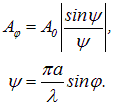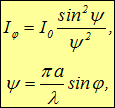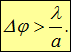5.4. Дифракция Фраунгофера от щели

Пусть на бесконечно длинную щель падает плоская световая волна. В соответствии с принципом Гюйгенса — Френеля освещенную щель можно рассматривать как множество точечных когерентных источников волн. Поместим за щелью экран, расстояние до которого достаточно велико по сравнению с шириной щели. Это условие означает, что в данную точку Р экрана попадет параллельный пучок лучей, отклонившийся на угол  (рис. 5.5).

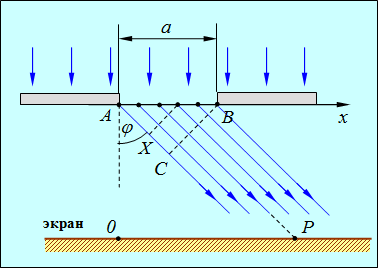
Рис. 5.5. Дифракция Фраунгофера от щели

Видео 5.10 Дифракция Фраунгофера. Щель и непрозрачная полоска.

Видео 5.11 Дифракция Фраунгофера. Две щели

Видео 5.12 Трехсантиметровые волны: дифракция Френеля на двух щелях

Видео 5.13 Трехсантиметровые волны: очень узка щель: d < α

Разность хода  крайних лучей из этого пучка определяется из треугольника  (угол ):

где а = АВ — ширина щели. Если при наблюдении из точки Р в щели помещается четное число зон Френеля (), то их вклады взаимно погасятся и в точке Р будет наблюдаться минимум интенсивности света. Таким образом, уравнение

дает условие дифракционных минимумов, где угол  — направление на минимум с номером k.

Если разность хода крайних лучей равна нечетному числу полуволн

то при наблюдении из точки Р в щели помещается нечетное число зон Френеля. Каждая зона гасит соседнюю, а оставшаяся последняя посылает свет в направлении  и образует максимум. Поэтому условие максимумов имеет вид

Соображения, приводящие к выражениям (5.21) и (5.22), имеют, вообще говоря, приближенный характер, поскольку мы применили метод зон Френеля для бесконечно удаленных точек наблюдения, рассматривая дифракцию в параллельных лучах, однако, как мы вскоре убедимся, условие минимумов (5.21) оказывается точным.

Что же касается центральной точки 0 экрана, расположенной против центра щели, то в нее попадает пучок неотклоненных лучей, ортогональных щели. Все они имеют одинаковую фазу, то есть должны усиливать друг друга. Поэтому в условии минимумов (5.21) исключено значение k = 0, соответствующее точке 0.

Значение k = 0 исключено и из условия максимумов (5.22), поскольку оно дает величину угла

так что этот максимум должен был бы расположиться между центральным максимумом  и первым минимумом

что невозможно.

После этих качественных соображений изучим дифракционную картину более подробно и получим выражения, позволяющие сравнить интенсивности света в максимумах различных порядков. Результирующее колебание в некоторой точке Р экрана представляет собой суперпозицию колебаний, распространяющихся от всей поверхности щели. В случае дифракции Фраунгофера расстояние от точки наблюдения до щели можно считать приблизительно постоянным при малых углах . Коэффициент  в формуле (5.2) также можно считать постоянным, если мы ограничимся рассмотрением не слишком больших углов дифракции . Обозначим А₀ суммарную амплитуду колебаний, возбуждаемых щелью в центральной точке 0 экрана. Поскольку щель бесконечно длинная, разобьем ее на полоски шириной dx так, чтобы вместо интегрирования по поверхности S (см. формулу (5.2)) перейти к интегрированию по координате х вдоль ширины щели. Тогда амплитуда колебаний, возбуждаемых элементом щели dx, будет равна

Такой же будет амплитуда колебаний, возбуждаемых этим же элементом в любой другой точке Р. Однако, если этот элемент находится в точке с координатой х (начало координат мы поместим в крайнюю точку А щели), то вторичная волна, дошедшая от него до точки Р, будет опережать по фазе колебание, дошедшее в Р от точки А. Разность фаз между рассматриваемыми колебаниями образуется на пути  (см. рис. 3.5). Если начальную фазу колебания, возбуждаемого в точке Р элементарной площадкой, расположенной в точке А, положить равной нулю, то начальная фаза колебания, возбуждаемого площадкой с координатой х, будет равна

где   — волновое число световой волны. Таким образом, учитывая (5.23) и (5.24), находим колебание, возбуждаемое в точке Р элементом щели с координатой х.

Проинтегрируем это соотношение по всей ширине щели (0<х<а) и получим результирующее колебание, возбуждаемое в точке Р.

Таким образом, амплитуда результирующего колебания имеет вид

Для точки 0, лежащей против центра щели, угол  и А = А₀. Этот результат следует, как мы видели, и из физических рассуждений.

Получим положение других максимумов. Для этого представим результирующую амплитуду в виде

Амплитуда имеет максимум при выполнении условия:

или

Очевидное решение  соответствует центральному максимуму. Следующий за ним корень уравнения (5.30), которое может быть решено только численно, равен . Отсюда находим условие первого максимума:

Из приближенного выражения (5.22) при k = 1 следует коэффициент 1.5 вместо правильного 1.43, что приводит к погрешности всего лишь в 5 %. Для других максимумов согласие с приближенной формулой становится еще лучше. Подозрительная же точка

соответствующая значению k = 0 в условии (5.22), не приводит к экстремуму амплитуды (5.27), как и следовало ожидать.

При углах , удовлетворяющих условию

амплитуда , как видно из (5.28), равна нулю. Это условие определяет положение минимумов, как и было получено выше в (5.21).

Интенсивность света пропорциональна квадрату амплитуды. Следовательно, из формулы (5.28) получаем

где I₀ — интенсивность в центре дифракционной картины, I - интенсивность в точке Р, положение которой определяется углом . Подставляя сюда , находим интенсивность I₁ в первом максимуме:

Иначе говоря, интенсивность в первом максимуме почти в 20 раз меньше, чем в центральном. Интенсивность в других максимумах будет еще меньшей.

Таким образом, центральный максимум дает главное изображение щели. В качестве меры его ширины можно принять расстояние между минимумами слева и справа от него. Используя условие первых минимумов

и учитывая, что при малых углах

получаем, что минимумы видны под углами

Поэтому угловой размер центрального максимума равен

Аналогичные формулы для отверстий другой формы отличаются лишь числовым коэффициентом. Отсюда следует общий вывод для любых оптических приборов. Если с помощью оптического прибора (микроскопа, подзорной трубы и т. п.) пытаются разглядеть два предмета, угловое расстояние между которыми равно , то это удастся сделать, если

Под α здесь надо понимать линейный размер отверстия прибора — его объектива (если объектив имеет диафрагму, то α — диаметр диафрагмы). Иначе изображения предметов (их центральные максимумы) попадут практически в одну и ту же точку, и предметы будет невозможно различить. Для повышения разрешающей способности прибора надо либо увеличить диаметр а объектива, либо использовать возможно более короткие волны. Последнее реализуется в электронных микроскопах.