2.2. Перемещение
Непрерывная линия, которую описывает точка при своем движении, называется траекторией.
Понятие траектории является существенно классическим и теряет привычный смысл в квантовой механике. В зависимости от формы траектории различают прямолинейное движение, движение по окружности и другие виды криволинейного движения.
Отметим, что кроме термина «материальная точка» удобно использовать полностью ему эквивалентный в данном контексте термин «частица». Пока не нужно ассоциаций с элементарными частицами: протонами, электронами, мезонами и так далее, их много. То есть частица — это просто другое слово для обозначения материальной точки.
Рис. 2.1. Траектория частицы. Радиус-вектор и перемещение
Положение материальной точки 
в пространстве задается радиус-вектором 
(см. п. 1.4). Поскольку мы рассматриваем движение точки, радиус-вектор зависит от времени:
Если в какой-то момент времени t1 положение материальной точки в пространстве было r = r(t1), а в момент времени t2 стало r = r(t2), то говорят о перемещении материальной точки из точки 1 в точку 2 (рис. 2.2.).
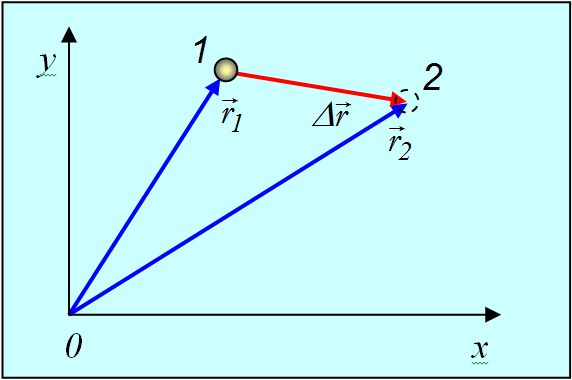
Рис. 2.2. Криволинейное движение частицы
Перемещение частицы за время от t1 до t2 — это вектор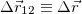 
, проведенный из положения частицы в момент времени t1 в ее положение в момент t2.
Из рис. 2.2. очевидно, что
Перемещение есть вектор характеризуется модулем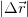 
и направлением, причем перемещения, как и положено векторам, складываются по правилу параллелограмма.
Важно отметить, что
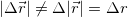
От перемещения следует отличать пройденный материальной точкой путь.
Путь за время от t1 до t2 — скалярная величина, равная длине участка траектории, пройденного материальной точкой за рассматриваемый промежуток времени.
Путь — неотрицательная, неубывающая функция времени. Может случиться так, что перемещение равно нулю, а путь достигает значительной величины. Например, вы утром выезжаете из гаража, ездите целый день по городу и к вечеру ставите машину на прежнее место. Поскольку начальное и конечное положения совпали (
), то перемещение равно нулю:
а пройденный путь отмечен на счетчике.
Чтобы вычислить пройденный путь, надо траекторию разбить на малые участки (рис. 2.3.).
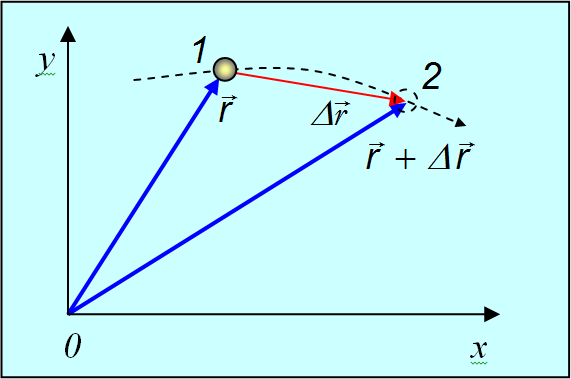
Рис. 2.3. Путь и перемещение при бесконечно малом перемещении
Тогда длина вектора перемещения 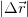будет приблизительно равна пройденному пути 
, причем совпадение будет тем точнее, чем мельче наше разбиение. При разбиении на бесконечно малые участки 
имеем равенство
Для нахождения полного пути 
надо просуммировать все эти бесконечно малые пути, то есть вычислить интеграл
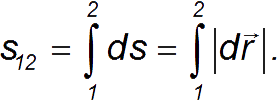
Здесь интегрирование ведется вдоль траектории от начальной точки 1 до конечной точки 2.
Интерактивная модель (рис. 2.4.) иллюстрирует разницу между путем и перемещением.
Рис. 2.4. Путь и перемещение
