2.3. Скорость
Скорость — векторная величина, характеризующая не только быстроту передвижения частицы по траектории, но и направление, в котором движется частица в каждый момент времени.
Средняя скорость за время от t1 до t2 равна отношению перемещения 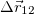 за это время к промежутку времени
за это время к промежутку времени 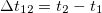 , за которое это перемещение имело место:
, за которое это перемещение имело место:
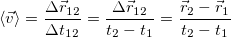
Тот факт, что это именно средняя скорость мы будем отмечать, заключая среднюю величину в угловые скобки: <...> , как это сделано выше.
Приведенная выше формула для среднего вектора скорости есть прямое следствие общего математического определения среднего значения <f(x)> произвольной функции f(x) на промежутке [a,b]:
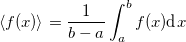
Действительно
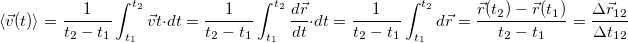
Средняя скорость может оказаться слишком грубой характеристикой движения. Например, средняя скорость за период колебаний всегда равна нулю, в независимости от характера этих колебаний, по той простой причине, что за период — по определению периода — колеблющееся тело вернется в исходную точку и, следовательно, перемещение за период всегда равно нулю. По этой и ряду других причин, вводится мгновенная скорость — скорость в данный момент времени. В дальнейшем, подразумевая мгновенную скорость, будем писать просто: «скорость», опуская слова «мгновенная» или «в данный момент времени» всегда, когда это не может привести к недоразумениям.Для получения скорости в момент времени t надо сделать очевидную вещь: вычислить предел отношения 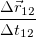 при стремлении промежутка времени t2 – t1 к нулю. Сделаем переобозначения: t1 = t и t2 = t +
при стремлении промежутка времени t2 – t1 к нулю. Сделаем переобозначения: t1 = t и t2 = t + 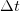 и перепишем верхнее соотношение в виде:
и перепишем верхнее соотношение в виде:
Скорость в момент времени t равна пределу отношения перемещения 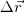 за время
за время 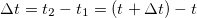 к промежутку времени, за которое это перемещение имело место, при стремлении последнего к нулю
к промежутку времени, за которое это перемещение имело место, при стремлении последнего к нулю
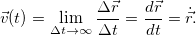

Рис. 2.5. К определению мгновенной скорости.
В данный момент мы не рассматриваем вопрос о существовании этого предела, предполагая, что он существует. Отметим, что если 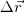 и
и 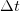 есть конечное перемещение и конечный промежуток времени, то
есть конечное перемещение и конечный промежуток времени, то 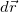 и
и 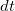 — их предельные величины: бесконечно малое перемещение и бесконечно малый промежуток времени. Так что правая часть определения скорости
— их предельные величины: бесконечно малое перемещение и бесконечно малый промежуток времени. Так что правая часть определения скорости
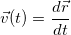
есть ничто иное как дробь — частное от деления 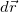 на
на 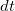 , поэтому последнее соотношение может быть переписано и весьма часто используется в виде
, поэтому последнее соотношение может быть переписано и весьма часто используется в виде
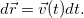
Здесь и далее мы часто для удобства будем использовать восходящее к Ньютону обозначение производной по времени в виде точки над соответствующей величиной:
![]()
По геометрическому смыслу производной, вектор скорости в каждой точке траектории направлен по касательной к траектории в этой точке в её сторону движения.
Видео 2.1. Вектор скорости направлен по касательной к траектории. Эксперимент с точилом.
Любой вектор можно разложить по базису (для единичных векторов базиса, другими словами, единичных векторов, определяющих положительные направления осей OX,OY,OZ используем обозначения 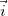 ,
, 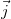 ,
, 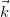 или
или 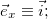
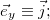
 , соответственно). Коэффициентами такого разложении являются проекции вектора на соответствующие оси. Важно следующее: в алгебре векторов доказано, что разложение по базису единственно. Разложим по базису радиус-вектор некоторой движущейся материальной точки
, соответственно). Коэффициентами такого разложении являются проекции вектора на соответствующие оси. Важно следующее: в алгебре векторов доказано, что разложение по базису единственно. Разложим по базису радиус-вектор некоторой движущейся материальной точки
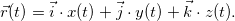
Учитывая постоянство декартовых единичных векторов 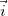 ,
, 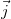 ,
, 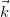 , продифференцируем это выражение по времени
, продифференцируем это выражение по времени
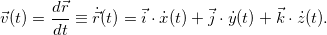
С другой стороны, разложение по базису вектора скорости имеет вид

опоставление двух последних выражений, с учетом единственности разложения любого вектора по базису, дает следующий результат: проекции вектора скорости на декартовы оси равны производным по времени от соответствующих координат, то есть
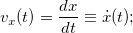
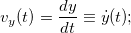
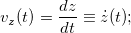
Модуль вектора скорости равен
![]()
Получим ещё одно, важное, выражение для модуля вектора скорости.
Уже отмечалось, что при ![]() величина |
величина |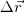 | все меньше и меньше отличается от соответствующего пути
| все меньше и меньше отличается от соответствующего пути ![]() (см. рис. 2). Поэтому
(см. рис. 2). Поэтому
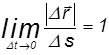
и в пределе (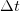 >0)
>0)
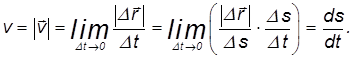
Иными словами, модуль скорости — это производная пройденного пути по времени.
Окончательно имеем:
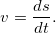
Средний модуль вектора скорости, определяется следующим образом:
Среднее значение модуля вектора скорости равно отношению пройденного пути ко времени, в течение которого этот путь был пройден:
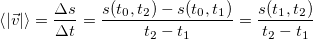
Здесь s(t1, t2) — путь за время от t1 до t2 и, соответственно, s(t0, t2) — путь за время от t0 до t2 и s(t0, t2) — путь за время от t0 до t1.
Средний вектор скорости или просто средняя скорость, как указано выше, равен
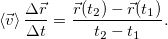
Отметим, что прежде всего, это вектор, его модуль — модуль среднего вектора скорости не следует путать со средним значением модуля вектора скорости. В общем случае они не равны: модуль среднего вектора вовсе не равен среднему модулю этого вектора 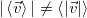 . Две операции: вычисление модуля и вычисление среднего, в общем случае, переставлять местами нельзя.
. Две операции: вычисление модуля и вычисление среднего, в общем случае, переставлять местами нельзя.
Рассмотрим пример. Пусть точка движется в одну сторону. На рис. 2.6. показан график пройденного ею пути s в от времени ![]() (за время от 0 до t). Используя физический смысл скорости, найти с помощью этого графика момент времени
(за время от 0 до t). Используя физический смысл скорости, найти с помощью этого графика момент времени ![]() , в который мгновенная скорость равна средней путевой скорости за первые
, в который мгновенная скорость равна средней путевой скорости за первые ![]() секунд движения точки.
секунд движения точки.
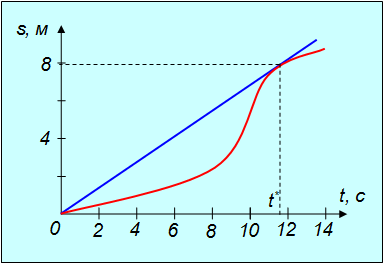
Рис. 2.6. Определение мгновенной и средней скорости тела
Модуль скорости в данный момент времени ![]()
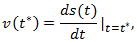
будучи производной пути по времени, равен угловому коэффициенту качательной к графику зависисмости ![]() точке соответствующей моменту времени t*. Средний модуль скорости
точке соответствующей моменту времени t*. Средний модуль скорости 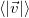 за промежуток времени от 0 до t* есть угловой коэффициент секущей, проходящей через точки того же графика, соответствующие началу t = 0 и концу t = t* временного интервала. Нам надо найти такой момент времени t*, когда оба угловых коэффициента совпадают. Для этого через начало координат проводим прямую, касательную к траектории. Как видно из рисунка точка касания этой прямой графика s(t) и дает t*. В нашем примере получается
за промежуток времени от 0 до t* есть угловой коэффициент секущей, проходящей через точки того же графика, соответствующие началу t = 0 и концу t = t* временного интервала. Нам надо найти такой момент времени t*, когда оба угловых коэффициента совпадают. Для этого через начало координат проводим прямую, касательную к траектории. Как видно из рисунка точка касания этой прямой графика s(t) и дает t*. В нашем примере получается ![]()



