2.6. Ускорение при криволинейном движении

Представим себе материальную точку, движущуюся по некоторой криволинейной траектории 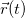. Запишем скорость в виде

и заметим, что вектор

— это единичный вектор, касательный к траектории и совпадающий по направлению с вектором скорости. Продифференцируем вектор скорости, записанный в данном представлении, и получим

Мы представили ускорение в виде двух слагаемых. Заметим прежде всего, что слагаемые ортогональны друг другу. Действительно, поскольку вектор — единичный, то

Дифференцируя это скалярное произведение, получаем

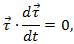
то есть

по свойству скалярного произведения.

Таким образом, мы разложили ускорение на сумму двух взаимно ортогональных составляющих, обозначем их 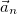и :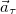

Обсудим физический смысл каждого слагаемого. Слагаемое

— это тангенциальное ускорение, которое характеризует быстроту изменения модуля скорости. Эта часть полного ускорения направлена либо по скорости, когда производная dv/dt > 0, то есть движение ускоренное, либо в сторону противоположную скорости, когда эта производная dv/dt < 0, то есть движение замедленное. Если движение равномерное dv/dt = 0, то есть скорость, если и меняется, то лишь по направлению, то тангенциальная часть ускорения равна нулю:

Слагаемое

направлено по нормали к траектории — перпендикулярно касательной к траектории и называется нормальным ускорением. Если тангенциальное ускорение определяет скорость, с которой меняется модуль вектора скорости, то нормальное ускорение определяет скорость, с которой меняется направление вектора скорости.

Рис. 2.10. К определению кривизны траектории

Рассмотрим «достаточно гладкую», в остальном произвольную плоскую криволинейную траекторию. Плоскую, то есть все точки траектории лежат в некоторой плоскости, — исключительно для упрощения выкладок, получаемый в рамках этого предположения, результат годится и для любой «достаточно гладкой» пространственной кривой, чьи точки уложить в одну плоскость невозможно. Последнее обстоятельство мы здесь рассматривать не будем, оно строго доказывается методами аналитической геометрии. Слова «достаточно гладкая» означают, что кривая описывается непрерывной функцией, имеющей непрерывные первую и вторую производные. С точки зрения физических приложений, требование существования непрерывных первых двух производных фактически не является ограничением на форму траектории, так как практически всегда выполнено. Проще говоря, на траектории не должно быть "углов" типа показанного на рисунке 2.11.

Рис. 2.11.

Такую «гладкую» кривую на любом её бесконечно малом участке можно заменить (рис. 2.12) участком окружности некоторого радиуса. Радиус этой окружности, аппроксимирующей траекторию на её бесконечно малом участке в окрестности некоторой точки, принято называть радиусом кривизны траектории в этой точке. Центр этой окружности принято называть центром кривизны траектории в данной точке. Кривизной траектории называется величина C = 1/R. Подчеркнем, что радиус кривизны, как и центр кривизны траектории — её локальные характеристика: каждой точке траектории соответствует свой радиус кривизны и свой центр кривизны. Исключениями являются: 1) окружность, её радиус кривизны во всех её точках один и тот же и равен радиусу окружности, центр кривизны «один на всех» и совпадает с центром окружности, и 2) прямая, для любой точки прямой радиус кривизны бесконечен, а центр кривизны находится в бесконечно удаленной от прямой точке. Это легко понять: давайте увеличивать радиус окружности, чем больше радиус окружности, тем ближе любой её конечный участок к участку прямой. На равнине, лучше всего на пляже, с высоты человеческого роста до горизонта не более пяти километров, — в этих пределах Земля плоская.

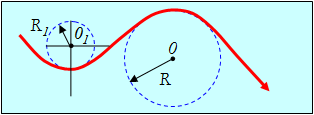
Рис. 2.12. К определению радиуса кривизны траектории

Вычислим модуль производной 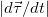, входящей в выражение для нормального ускорения. Направлен вектор 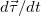по нормали к траектории к центру к центру кривизны, что поясняет рис. 2.13.

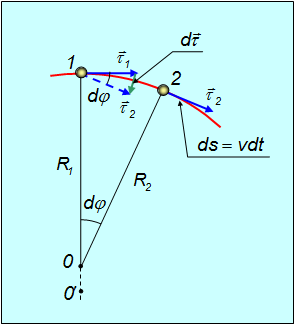
Рис. 2.13. Графическое определение радиуса кривизны траектории

Для этого прежде всего перейдем от дифференцирования по времени к дифференцированию по «пути»: 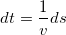, имеем:

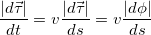
По определению производная 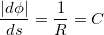кривизне кривой C, а величина ей обратная равна радиусу кривизны кривой R. Собирая всё вместе, для нормального ускорения 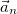окончательно получаем:

,

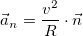где нормаль 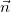перпендикулярна к касательной 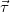и всегда направлена к центру кривизны, см. рис. 11.

Приведем некоторое дополнительное пояснение к рисунку 11. Возьмем неподалеку от точки 1 точку 2. Построим в этих точках касательные единичные векторы ₁ и ₂. Перпендикуляры к этим касательным пересекутся в некоторой точке O₂. Заметим, что для кривой, не являющейся окружностью, расстояния R₁ и R₂ будут немного отличаться друг от друга. Если теперь точку 2 приближать к точке 1, пересечение перпендикуляров O₂ будет перемещаться вдоль прямой O₂1 и в пределе окажется в некоторой точке O₁. Расстояния R₁ и R₂ будут стремиться к общему пределу R, равному радиусу кривизны, а точка O₁ и будет центром кривизны для точки 1. Действительно, окружность радиусом R с центром в 0 проходит через точку 1 и касается траектории (так как радиус ортогонален орту ₁). Кроме того, по построению бесконечно близкая точка 2 также лежит на этой окружности. Таким образом, построенная окружность действительно «сливается» с траекторией в точке 1.

Итак, в общем случае ускорение имеет две составляющие — тангенциальную

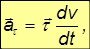
направленную вдоль касательной и определяющую скорость изменения модуля вектора скорости нормальную

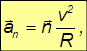
направленную перпендикулярно скорости к центру кривизны траектории и пропорциональную угловой скорости вращения вектора скорости при движении частицы вдоль криволинейной траектории (рис. 2.14).

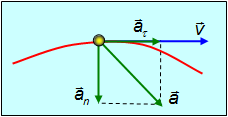
Рис. 2.14. Тангенциальное и нормальное ускорения при ускоренном криволинейном движении.

Действительно 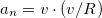, где 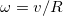и есть угловая скорость вращения вектора скорости .

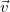Полное ускорение

определяется по правилу параллелограмма. Модуль полного ускорения в соответствии с теоремой Пифагора равен

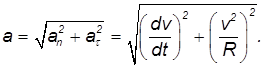
Выпишем без вывода формулы, связывающие радиус кривизны плоской траектории с координатами траектории. Если известна зависимость y = y(x), то

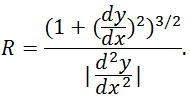
Если же траектория задана в параметрическом виде, x = x(t), y = y(t), то

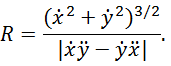
Пример криволинейного движения с постоянным ускорением (тело, брошенное под углом к горизонту) приведен на следующем рисунке:

Рис. 2.15. Движение тела, брошенного под углом к горизонту