2.5. Ускорение

Скорость частицы может изменяться со временем, как по величине, так и по направлению.

Быстрота (скорость) изменения во времени любой величины определяется производной по времени от этой величины. Это общее правило касается и вектора скорости.

Ускорение равно производной вектора по времени t, или, что то же самое — второй производной по времени радиус-вектора :

Рис. 2.9. Тангенциальное и нормальное ускорения.

Если известны зависимость от времени ускорения а = a(t) и начальная скорость v₀ (при t = t₀), то значение скорости в любой момент времени t равно

Если известно также положение 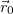тела в начальный момент t = t₀ , то мы можем найти не только скорость, но и положение тела в любой момент времени:

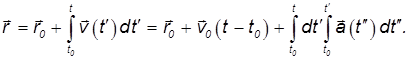
При равноускоренном движении ( ) интегралы легко вычисляются и мы получаем:

Вычисление последнего интеграла приводит к закону равноускоренного движения материальной точки

При прямолинейном движении векторы перемещения, скорости и ускорения направлены вдоль одной и той же прямой, совпадающей с траекторией. Поэтому направление прямой можно принять за ось x и оперировать с ускорением и скоростью как с проекциями векторов на эту ось, то есть как с алгебраическими величинами. При этом индекс, обозначающий проекцию вектора на ось, опускают.

Видео 2.2. Скатывание тележки с наклонной плоскости как пример равноускоренного движения.