3.6. Реактивное движение
Рассмотрим движение тела, масса которого меняется в процессе движения, на примере движения ракеты.
Принцип движения ракеты заключается в том, что продукты сгорания топлива с большой скоростью выбрасываются из ракеты, толкая ее при этом в противоположную сторону.
Заметим, что при движении ракеты ее масса непрерывно изменяется, следовательно, второй закон Ньютона в рассмотренной ранее форме для описания движения ракеты неприменим.
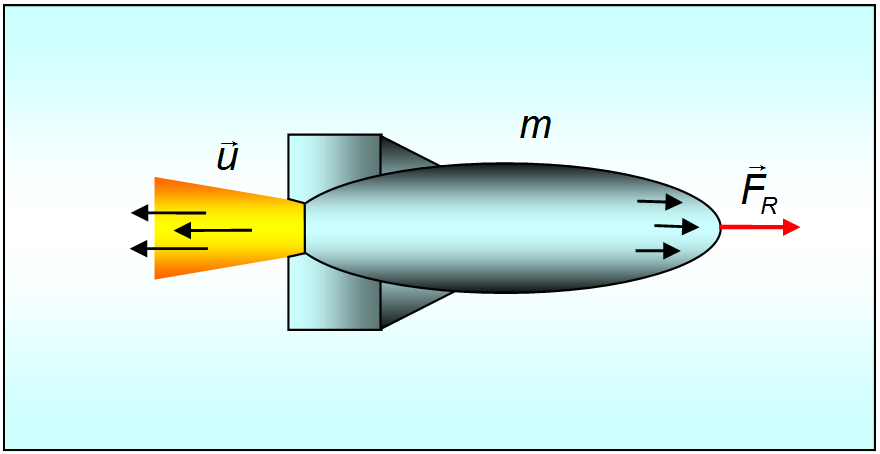
Рис. 3.30. Принцип движения ракеты
Пусть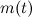 
— масса ракеты в момент 
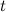, а 
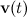— ее скорость. Импульс ракеты будет
За время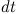 
масса ракеты и ее скорость получают приращения 
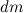(причем 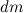< 0), так как масса ракеты убывает) и 
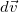соответственно, так что к моменту времени 
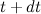они будут равны
Импульс ракеты станет
Кроме этого следует учесть импульс выброшенных за время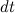 
газов:
где 
— масса выброшенных за время 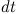газов, 
— их скорость относительно Земли.
Воспользуемся вторым законом Ньютона в импульсной форме. Тогда
Раскроем скобки,учитывая, что 
(масса ракеты уменьшилась на массу выброшенных из сопла двигателя газов):
Введем u — скорость истечения газовой струи относительно ракеты. Тогда
После преобразований и удержания членов первого порядка малости (член второго порядка малости 
отброшен) получаем
или
Данное уравнение по форме напоминает второй закон Ньютона, однако здесь возникает дополнительное слагаемое
называемое реактивной силой. C учетом этого уравнение движения принимает вид
Это уравнение движения тела переменной массы носит название уравнения Мещерского.
Величина
называется расходом топлива.
Рассмотрим движение ракеты в отсутствие внешних сил (F = 0) (рис. 3.31). Спроецируем уравнение Мещерского на направление движения ракеты 
:
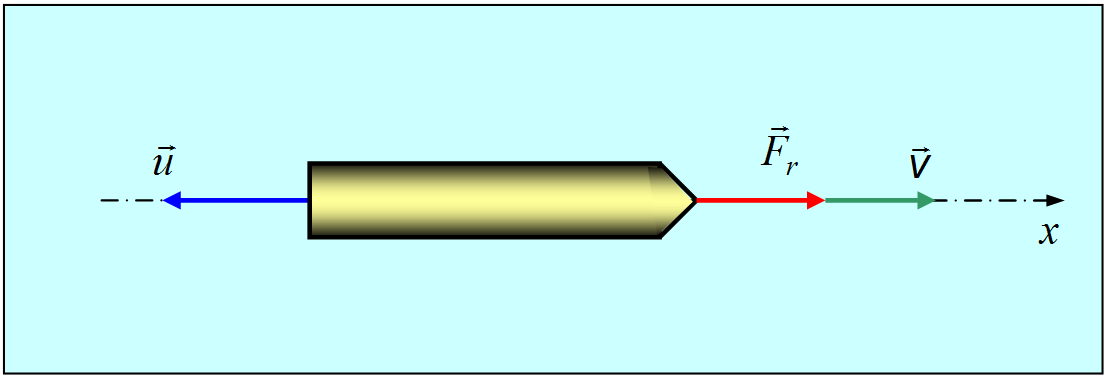
Рис 3.31. Движение ракеты в отсутствие внешних сил
С учетом, что
получаем
Разделим переменные:
Обычно можно считать, что скорость истечения газов относительно ракеты постоянна. Интегрируя полученное уравнение, находим
Пусть в начальный момент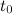 
= 0 мы имеем
и
Тогда
откуда находим постоянную интегрирования
Тогда формула для скорости ракеты, называемая формулой Циолковского, принимает вид
Ясно, что конечная скорость ракеты определяется скоростью истечения газовой струи, которая — в случае химического двигателя с реакцией окисления и выбросом продуктов реакции — зависит от температуры сгорания T и молярной массы газов M
.
Следовательно, наиболее эффективным топливом будет водород с очень высокой температурой сгорания и малой молярной массой. Водород как топливо нашел широкое применение в космонавтике, несмотря на повышенную пожароопасность и потребность (при хранении в баках ракеты) в очень низких (криогенных) температурах.
Пример. Пусть ракете необходимо сообщить первую космическую скорость 
= 8 км/с. Если использовать топливо со скоростью истечения 
= 1 км/с (порох), то отношение массы полезной нагрузки к стартовой массе ракеты будет
Если же использовать топливо с = 2 км/с (водород), то
Видно, что при одинаковой полезной нагрузке стартовая масса ракеты во втором случае будет почти в 50 раз меньше, чем в первом.
Дополнительная информация
http://kvant.mirror1.mccme.ru/1986/05/paradoks_sputnika.html — Журнал «Квант» – парадоксальное поведение спутника и ракеты-носителя в верхних слоях атмосферы Земли после их отделения друг от друга (Ю.Г. Павленко);
http://kvant.mirror1.mccme.ru/1971/07/paradoksy_reaktivnogo_dvizheni.html — Журнал «Квант» – КПД ракетного двигателя и парадоксы реактивного движения (М. Лившиц).
