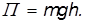5.5. Потенциальная энергия гравитационного взаимодействия

В пространстве, окружающем тела, что-то меняется: мы говорим, что они создают гравитационное поле. Энергетическая характеристика этого поля — потенциальная энергия взаимодействия двух гравитационных масс — определяется по общим правилам. Именно, градиент потенциальной энергии должен давать силу:

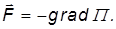
Для центральных сил

к которым относится и сила всемирного тяготения, это уравнение, как мы видели в предыдущем разделе, сводится к уравнению

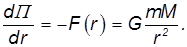
Отсюда

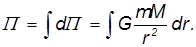
Интегрируя, получим

Постоянную интегрирования const принимают равной нулю, чтобы при , стремящемся к бесконечности, потенциальная энергия гравитационного взаимодействия стремилась к нулю. Это не умаляет общности, так как физически наблюдаемой является разность потенциальных энергий, а не ее значение.

Рассмотрим изменение потенциальной энергии тела 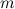, перемещенного с поверхности Земли на высоту :

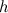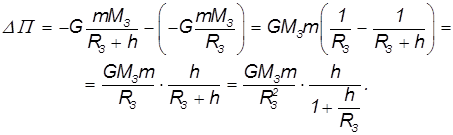
Учитывая, что

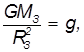
получаем

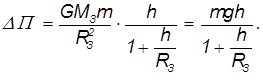
Если выбрать потенциальную энергию тела на поверхности Земли равной нулю, то 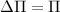. При малых высотах 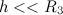можно пренебречь отношением 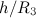в знаменателе правой части полученной формулы для потенциальной энергии, что дает знакомое выражение