6.1. Анализ преобразований Галилея

Рассмотрим две системы отсчета — инерциальную систему K (с координатами x, y, z ), которую условно будем считать неподвижной, и систему K' (с координатами x', y', z' ), движущуюся относительно K равномерно и прямолинейно со скоростью v (для конкретности вдоль оси x ). Отсчет времени начнем с момента, когда начала координат обеих систем совпадают (рис. 6.1).

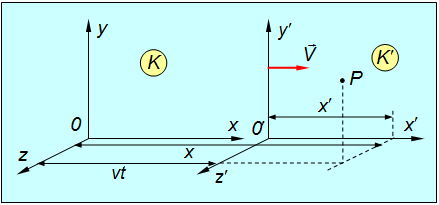
Рис. 6.1. Преобразования Галилея при переходе из одной инерциальной системы отсчета в другую

Ранее мы уже нашли связь между координатами произвольной точки P в обеих системах отсчета:

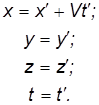
Эти уравнения носят название преобразований Галилея. В классической механике предполагается, что ход времени не зависит от относительного движения систем отсчета, то есть к преобразованиям координат мы добавили еще и уравнение совпадения времен.

Продифференцировав преобразования Галилея по времени с учетом

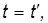
мы получаем правило сложения скоростей по Галилею в векторной форме:

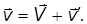
Дифференцируя еще раз, находим соотношение для ускорений — ускорение a в системе К оказывается равным ускорению а' в системе К' :

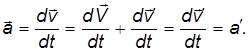
Еще раз: ускорение какого-либо тела во всех системах отсчета, движущихся друг относительно друга прямолинейно и равномерно (то есть V = const), оказывается одним и тем же. Как говорят, ускорения инвариантны относительно таких систем отсчета. Поэтому, если одна из них инерциальная, то и остальные системы отсчета также будут инерциальными.

Как следствие, никакими механическими опытами невозможно установить, покоится данная система отсчета или движется прямолинейно и равномерно. Иными словами, в природе отсутствует выделенная система отсчета.

Инвариантность длины и интервала времени. Расстояние между двумя точками P₁ и P₂ можно выразить через координаты этих точек в системе К :

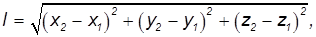
и именно это расстояние измеряет наблюдатель в системе отсчета К. Для наблюдателя же в системе отсчета К' координаты тех же точек будут другими, и он определит расстояние между ними как

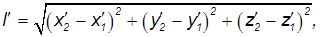
Из преобразований Галилея следует, что

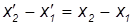
и аналогично для других координат, так что

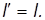
Иными словами, оба наблюдателя находят одно и то же значение для расстояния между двумя точками — длина инвариантна по отношению к преобразованиям Галилея.

Аналогичным образом, очевидно, инвариантны интервалы времени для обоих наблюдателей:

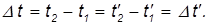
Если два события одновременны (t₁ = t₂), то временной интервал между ними равен нулю. Вследствие инвариантности это же справедливо и в системе отсчета К', то есть данные события одновременны в любой инерциальной системе отсчета.

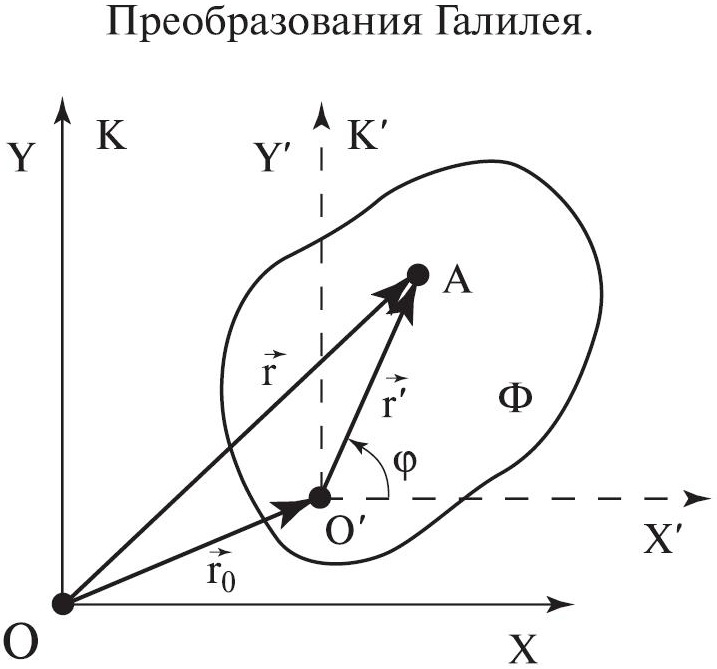
Рис. 6.2. Преобразования Галилея в общем случае

Задумаемся, откуда взялись столь естественные на первый взгляд утверждения? Преобразования Галилея для координат следуют из простого геометрического правила сложения векторов. Но посмотрим на этот рисунок внимательнее. Вектор r' в сущности задан относительно системы К', наблюдатель в этой системе описывает им положение некоторой точки в пространстве. Наблюдатель в системе отсчета К предполагает, что может использовать этот же радиус-вектор, чтобы сложить с радиус-вектором начала отсчета 0' и получить положение той же точки относительно системы К. Но на чем основано это предположение? На том, что вектор r' одинаков в обеих системах отсчета, что у него в обеих системах те же проекции на координатные оси и та же длина. А это значит, что при выводе преобразования Галилея мы изначально неявно предположили инвариантность расстояний. Инвариантность же интервалов времени мы постулировали совершенно откровенно. Основанием для этого служит наш повседневный опыт. Но любой опыт ограничен какими-то масштабами, в пределах которых он приобретен. Когда ученые столкнулись с физикой больших скоростей при изучении распространения электромагнитных волн (света) оказалось, что наш повседневный опыт более не применим.

Дополнительная информация

http://ilib.mirror1.mccme.ru/djvu/bib-kvant/kvant_59.djvu — Чернин А.Д. Физика времени, библиотечка Квант, выпуск 59, главы 3, 12 — о часах, времени и энергии.