6.10. Частицы с нулевой массой
Рассмотрим релятивистское выражение, связывающее энергию и импульс:
![]()
Положив в этом соотношении ![]() , получим
, получим
![]()
С другой стороны, модуль импульса частицы связан с ее скоростью соотношением
![]()
Подставляя сюда полученное выражение для энергии частицы с нулевой массой, получаем ![]() . Частицы нулевой массы не могут покоиться и не могут двигаться иначе как со скоростью света! К числу таких частиц принадлежит световая частица, называемая фотоном (обозначается символом
. Частицы нулевой массы не могут покоиться и не могут двигаться иначе как со скоростью света! К числу таких частиц принадлежит световая частица, называемая фотоном (обозначается символом ![]() ), a также нейтрино (обозначается
), a также нейтрино (обозначается ![]() ). У таких частиц нет энергии покоя
). У таких частиц нет энергии покоя ![]() , так как они никогда не покоятся. Но энергией они обладают, что каждый может ощутить на практике, загорая на пляже. На рис. 10 это соответствует предельному случаю, когда нижний катет равен нулю, а гипотенуза совпадает с другим катетом и кинетической энергией:
, так как они никогда не покоятся. Но энергией они обладают, что каждый может ощутить на практике, загорая на пляже. На рис. 10 это соответствует предельному случаю, когда нижний катет равен нулю, а гипотенуза совпадает с другим катетом и кинетической энергией: ![]() .
.
Пример. Элементарная частица, называемая нейтральным пи-мезоном (обозначение ![]() ) распадается на два фотона:
) распадается на два фотона:
![]()
Определим импульсы фотонов, если распавшийся пи-мезон покоился. Масса частицы ![]() кг.
кг.
Так как вначале пи-мезон покоился, полный импульс системы был равен нулю. Вследствие закона сохранения импульсы фотонов ![]() равны по величине и направлены в противоположные стороны. Следовательно, равны и энергии фотонов
равны по величине и направлены в противоположные стороны. Следовательно, равны и энергии фотонов ![]() . Записываем закон сохранения энергии в этой реакции:
. Записываем закон сохранения энергии в этой реакции:
![]()
откуда импульсы фотонов равны
![]()
При этом энергия каждого фотона равна половине энергии покоя пи-мезона.
В дальнейшем мы узнаем, что энергия фотона связана с частотой световой волны ![]() соотношением
соотношением
![]()
Фотон обладает также импульсом
![]()
Падая на поверхность, фотоны передают ей свой импульс и оказывают тем самым давление. Обнаружить и измерить световое давление удалось П.Н. Лебедеву в 1900 г.
В 1916 г. А. Эйнштейн, обобщая идеи специальной теории относительности (СТО) на неинерциальные системы, создал теорию гравитации, которую называют также общей теорией относительности — ОТО. Согласно этой теории, любой объект, обладающий энергией ![]() , будет подвержен действию гравитационного поля как если бы он имел гравитационную массу
, будет подвержен действию гравитационного поля как если бы он имел гравитационную массу ![]() . Связь
. Связь ![]() с энергией тела дается уже знакомым соотношением
с энергией тела дается уже знакомым соотношением
![]()
Масса фотона равна нулю, но в любом гравитационном поле он должен вести себя как частица с гравитационной массой
![]()
При движении фотона вблизи поверхности Земли вверх по вертикали фотон должен затратить часть своей энергии на совершение работы против сил тяжести:
![]()
где ![]() — пройденный по вертикали путь. Соответственно первоначальная энергия фотона, равная
— пройденный по вертикали путь. Соответственно первоначальная энергия фотона, равная
![]()
должна уменьшиться на величину ![]() . Значит, частота фотона в конце пути будет меньше на величину
. Значит, частота фотона в конце пути будет меньше на величину ![]() :
:
![]()
Относительное уменьшение частоты фотона
![]()
при распространении по вертикали было измерено в 1960 г. американскими учеными Паундом и Ребкой. В условиях опыта оно составило малую величину, равную ![]() . Значит, перепад высот в опыте Паунда — Ребки составлял
. Значит, перепад высот в опыте Паунда — Ребки составлял
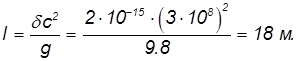
Эффект изменения частоты света при удалении от большой тяготеющей массы называется гравитационным красным смещением.
Дополнительная информация
Детальный анализ данного эффекта можно найти в статье: Л.Б. Окунь, К.Г. Селиванов, В.Л. Телегди, «Гравитация, фотоны, часы», УФН 169, 10, стр. 1141 (1999).
http://ufn.ru/ufn01/ufn01_12/Russian/r0112d.pdf — журнал УФН — из истории физики — об открытии уравнений гравитационного поля (В.П. Визгин).


