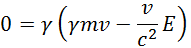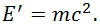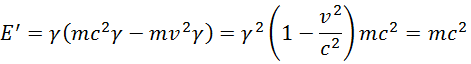6.9. Полная энергия тела
В теории относительности пространство и время не являются более независимыми: из преобразований Лоренца и инвариантности интервала видно, что они входят в уравнения на равных правах, образуя единое пространство-время. Вспомним, что законы сохранения импульса ![]() и энергии
и энергии ![]() тела связаны с однородностью пространства и времени, соответственно. При переходе к движущейся системе отсчета выражения для импульса и энергии должны преобразовываться аналогично координатам и времени в преобразованиях Лоренца. Выполненные ниже на базе аналогий и анализа размерностей преобразования не являются вполне строгими, но приводят к правильному результату. Строгие выкладки требуют использования аппарата 4х-векторов в четырехмерном пространственно-временном континууме, что выходит за рамки наших нынешних задач. Посмотрим на уравнения, описывающие преобразования Лоренца
тела связаны с однородностью пространства и времени, соответственно. При переходе к движущейся системе отсчета выражения для импульса и энергии должны преобразовываться аналогично координатам и времени в преобразованиях Лоренца. Выполненные ниже на базе аналогий и анализа размерностей преобразования не являются вполне строгими, но приводят к правильному результату. Строгие выкладки требуют использования аппарата 4х-векторов в четырехмерном пространственно-временном континууме, что выходит за рамки наших нынешних задач. Посмотрим на уравнения, описывающие преобразования Лоренца
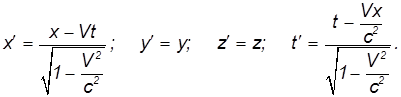
Если заменить в первом из них
![]()
то время ![]() надо заменить на величину, пропорциональную энергии в системе отсчета
надо заменить на величину, пропорциональную энергии в системе отсчета ![]() . Коэффициент пропорциональности следует из соображений размерности: энергию надо разделить на квадрат какой-то скорости. У нас есть лишь одна выделенная скорость — скорость света. Аналогично, в последнем уравнении меняем
. Коэффициент пропорциональности следует из соображений размерности: энергию надо разделить на квадрат какой-то скорости. У нас есть лишь одна выделенная скорость — скорость света. Аналогично, в последнем уравнении меняем
![]()
а координату ![]() — на величину, пропорциональную импульсу
— на величину, пропорциональную импульсу ![]() . В результате записываем преобразования Лоренца для импульса и энергии в системах отсчета
. В результате записываем преобразования Лоренца для импульса и энергии в системах отсчета ![]() и
и ![]() :
:
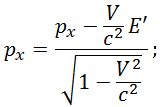
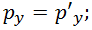
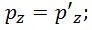
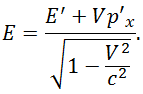
Обратные преобразования имеют вид:
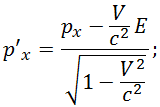

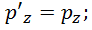
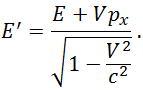
Или, короче, с использованием релятивистского фактора 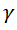
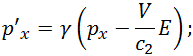
|
(6.9.1) |
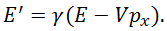
Что такое релятивистский импульс — мы уже знаем. Но что такое релятивистская энергия ![]() ? Именно эта величина выступает партнером импульсу в преобразованиях Лоренца для импульса и энергии, именно она связана со свойствами пространства-времени и должна сохраняться в замкнутых системах. Применим полученные формулы к точке массой
? Именно эта величина выступает партнером импульсу в преобразованиях Лоренца для импульса и энергии, именно она связана со свойствами пространства-времени и должна сохраняться в замкнутых системах. Применим полученные формулы к точке массой ![]() , движущейся вдоль оси
, движущейся вдоль оси ![]() с постоянной скоростью
с постоянной скоростью ![]() . Ее импульс равен
. Ее импульс равен
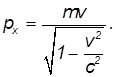
Свяжем с точкой систему отсчета ![]() . В этой системе точка покоится, то есть
. В этой системе точка покоится, то есть ![]() . Подставим эти соотношения в первую из формул (6.9.1)
. Подставим эти соотношения в первую из формул (6.9.1)
|
(6.9.2) |
Откуда для энергии частицы массы m, движущейся в нашей системе отсчета со скоростью v, получаем
|
(6.9.3) |
В системе отсчета, в которой частица покоится, как следует из (6.9.3), её энергия равна
|
(6.9.4) |
Результат (6.9.4) можно получить и так. В последнюю из формул (6.9.1) подставим импульс p = mvγ и энергию E = mc2γ из (6.9.3), получаем
|
(6.9.5) |
Мы получили очень интересные результаты. В системе ![]() точка покоится, но ее энергия отлична от нуля. Ее так и называют — энергия покоя и обозначают
точка покоится, но ее энергия отлична от нуля. Ее так и называют — энергия покоя и обозначают ![]()
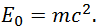
Мы пришли к знаменитой формуле Эйнштейна. Полная энергия движущегося тела дается суммой энергий покоя и кинетической энергии
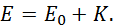
Энергия покоя, сосредоточенная в теле, огромна. Для примера: килограмм угля при сжигании дает около 30 МДж = 3·107 Дж энергии. Энергия же покоя того же килограмма равна ![]() Дж, то есть в три миллиарда раз больше. При некоторых условиях энергия покоя может быть выделена. К сожалению, на практике это впервые было осуществлено при взрыве атомной бомбы.
Дж, то есть в три миллиарда раз больше. При некоторых условиях энергия покоя может быть выделена. К сожалению, на практике это впервые было осуществлено при взрыве атомной бомбы.
Из релятивистских выражений для импульса 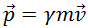 и энергии
и энергии 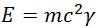 нетрудно получить связь между ними:
нетрудно получить связь между ними:
![]()
Отсюда следует, что левая часть полученного выражения является инвариантом, то есть не зависит от системы отсчета. Это же можно получить из преобразований Лоренца. Итак, зная импульс тела, можно найти его энергию
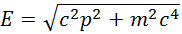
и скорость
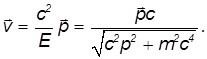
Связь кинетической энергии с импульсом:
![]()
Релятивистские соотношения между энергией тела, его импульсом и скоростью можно изобразить графически в виде прямоугольного треугольника (рис. 6.15), облегчающего запоминание формул.
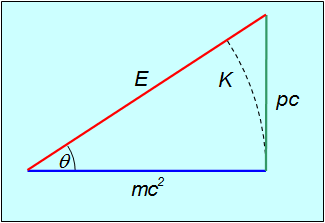
Рис. 6.15. Графическое представление соотношения между энергией и импульсом тела
При бесконечно больших импульсах энергия тела неограниченно растет, а скорость стремится к скорости света. Наоборот, при малых импульсах имеем:
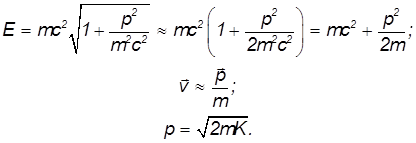
Мы снова пришли к нерелятивистским соотношениям для кинетической энергии и скорости частицы как функций ее импульса.
Из всего сказанного следуют критерии применимости классической механики Ньютона — Галилея:
![]()
или
![]()
или
![]()
Все выписанные соотношения эквивалентны, из любого из них следуют остальные.
Пример. Солнечная постоянная C (плотность падающего на Землю потока энергии излучения Солнца) равна ![]() . Определим массу
. Определим массу ![]() , которую теряет Солнце за один год.
, которую теряет Солнце за один год.
Земля находится от Солнца на расстоянии ![]() м. За время
м. За время ![]() на единицу площади попадает энергия
на единицу площади попадает энергия ![]() . Умножая на площадь сферы радиусом
. Умножая на площадь сферы радиусом ![]() , получаем полную энергию, излученную Солнцем за время
, получаем полную энергию, излученную Солнцем за время ![]() :
:
![]()
Эта энергия возникает в результате термоядерных реакций за счет уменьшения энергии покоя Солнца. Следовательно, его масса за год уменьшится на величину
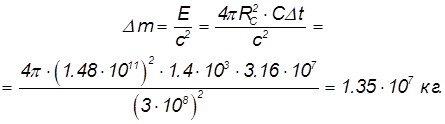
За время своего существования (5 млрд лет) Солнце потеряло в массе ![]() кг. Учитывая, что масса Солнца равна
кг. Учитывая, что масса Солнца равна ![]() кг, потери массы на излучение составляют 0,03 %. Пример демонстрирует важный вывод теории относительности:
кг, потери массы на излучение составляют 0,03 %. Пример демонстрирует важный вывод теории относительности:
В природе нет закона сохранения массы, есть лишь закон сохранения полной энергии.
Закон сохранения массы возник в классической физике только потому, что кинетические энергии продуктов химических реакций в сотни миллионов раз меньше их энергий покоя. Так что, в химических реакциях масса сохраняется с точностью порядка миллионных долей процента.
Дополнительная информация
http://kvant.mirror1.mccme.ru/1995/02/prostoj_vyvod_formuly.htm — журнал «Квант» — простой вывод формулы E = mc2 (Б. Болотовский).
http://ufn.ru/ufn89/ufn89_7/Russian/r897f.pdf — журнал УФН — подробно обсуждается вопрос о понятии массы в нерелятивистской и релятивистской физике (Л.Б. Окунь).
http://ufn.ru/ru/articles/2000/12/i/ — журнал УФН — дискуссия о понятии массы (Р.И. Храпко).
http://ufn.ru/ufn00/ufn00_12/Russian/r0012g.pdf — журнал УФН – дискуссия о понятии массы (Л.Б. Окунь).
http://eqworld.ipmnet.ru/ru/library/physics/relativity.htm — Угаров В.А. Специальная теория относительности, Наука, 1977. — стр. 338–342, дополнение IV — обсуждается, почему не следует вводить зависимость массы от скорости или же релятивистскую массу.
http://eqworld.ipmnet.ru/ru/library/physics/relativity.htm — Угаров В.А. Специальная теория относительности, Наука, 1977. — стр. 162–168 (§ 5.7) — задача V, реактивное движение в релятивистской механике; — задача VI, энергия взаимодействия элементарных частиц в ускорителе на встречных пучках.
http://www.femto.com.ua/articles/part_1/2157.html — физическая энциклопедия. В статье раскрыто физическое содержание фундаментальной величины — массы тела.