6.8. Релятивистское выражение для кинетической энергии

Итак, релятивистское уравнение движения материальной точки, или основное уравнение релятивистской динамики, имеет обычный вид уравнения второго закона Ньютона, но с другой зависимостью импульса от скорости:

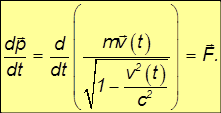
Преобразуем приращение импульса в левой части этого уравнения:

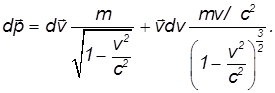
Умножим основное уравнение релятивистской динамики скалярно на вектор перемещения

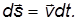
Справа мы имеем обычное выражение для изменения кинетической энергии тела:

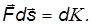
Слева после учета, что

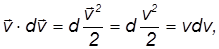
можно получить

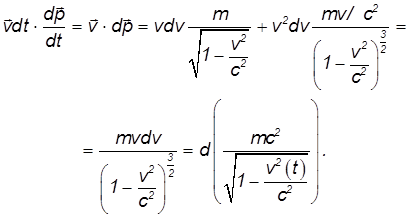
Таким образом,

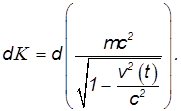
Следовательно, выражение в скобах справа с точностью до постоянной интегрирования представляет собой кинетическую энергию материальной точки, движущейся со скоростью v. Значение этой постоянной фиксируется условием, что К = 0 при v = 0.

Окончательно получаем релятивистское выражение для кинетической энергии

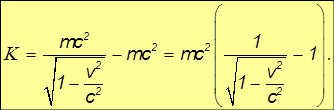
Или короче, используя релятивистский фактор :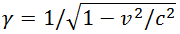

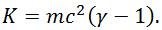
При малых скоростях v << с мы можем разложить квадратный корень в ряд Тейлора по степеням отношения v/c. Оставляя первые два члена ряда, имеем

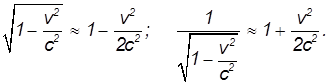
В этом приближении кинетическая энергия определяется классической формулой

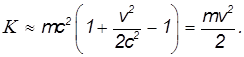
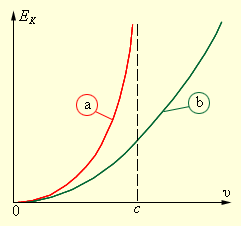
Рис. 6.14. Зависимость кинетической энергии от скорости. а – релятивистское значение, b – классическое значение кинетической энергии.