6.6. Аберрация света

Явление аберрации было открыто Дж. Бредли в 1725 г.: наблюдения показали, что в течение года звезды описывают на небе небольшие эллипсы. Период обращения звезд подсказал, что это явление связано с годовым движением Земли вокруг Солнца. Теоретическое объяснение основывалось на идее сложения скорости луча света от звезды с орбитальной скоростью Земли. Рассказывают, что толчком к пониманию эффекта послужила прогулка Бредли на яхте. Он заметил, что вымпел на мачте вовсе не указывает направления ветра, но меняет свое направление каждый раз при повороте яхты.

Пусть, к примеру, в гелиоцентрической системе отсчета свет от неподвижной в этой системе отсчета звезды М приходит на Землю под углом ψ к направлению движения Земли в момент приёма этого света земными детекторами (левая часть рис. 6.11). Ось ОХ выбранной системы отсчета направлена по вектору скорости Земли (красная стрелка на правой части рисунка).

Рис.6.11. Углы наблюдения звезды в различных системах отсчета

В системе отсчета K', связанной с Землей, угол наклона ψ' светового луча будет иным. Действительно, x-компоненты скорости луча света в системах K и K' равны соответственно

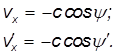
Здесь мы приняли во внимание, что модуль скорости света в обеих системах равен c. С другой стороны, компоненту скорости света в системе K' можно получить из релятивистского закона сложения скоростей

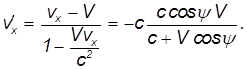
Приравнивая правые части выражений для v'_x находим

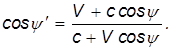
В течение года Земля в неподвижной системе отсчета описывает замкнутую траекторию, ее скорость меняется по величине и направлению, так что периодически меняется и угол наблюдения звезды ψ', в то время как угол ψ остается неизменным. Это и есть явление аберрации.

Применим теперь полученные формулы к случаю наблюдения звездного неба с гипотетического космического корабля, движущегося с большой скоростью. Представим себе, что звезды в неподвижной системе расположены равномерно на небосводе. С точки зрения астрономов на корабле это уже не так. Действительно, звезда сзади по курсу корабля не сдвинется: из наших формул при ψ = 180°, cos ψ = –1 следует, что cos ψ' = –1, ψ' = 180°. Звезда же, расположенная по углом ψ = 90° (cos ψ = 0) к курсу корабля будет наблюдаться космонавтами в направлении cos ψ' = V/c. При V близких к c этот угол очень мал. В этом узком конусе будут сосредоточены все звезды передней (в неподвижной системе отсчета) полусферы. Наоборот, можно показать, что звезды из узкого конуса с тем же углом раствора, но сзади по курсу, займут всю заднюю полусферу в системе отсчета K'. Таким образом, при увеличении скорости корабля небо позади остается почти пустынным, в то время как почти вся видимая Вселенная сольется в яркое пятно впереди по курсу.