7.4. Главные оси инерции твердого тела

Если какое-либо тело привести во вращение относительно произвольной оси и затем предоставить самому себе, то положение оси вращения в пространстве, вообще говоря, изменится: ось будет либо поворачиваться, либо перемещаться относительно инерциальной системы отсчета. Для того, чтобы произвольно взятую ось удерживать в неизменном положении, к ней необходимо приложить определенные силы.

Можно показать, что существуют по крайне мере три взаимно перпендикулярные оси, проходящие через центр масс тела, которые могут служить свободными осями. Такие оси называются главными осями инерции тела.

Для тел, обладающих осевой симметрией (например, у однородного цилиндра), одна из главных осей совпадает с осью симметрии, а две любые оси, перпендикулярные к оси симметрии и друг другу и проходящие через центр масс тела, также являются главными (рис. 7.15). Моменты инерции относительно двух последних осей равны друг другу, а момент инерции относительно оси симметрии отличен от них

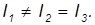
Такое тело называется симметричным волчком.

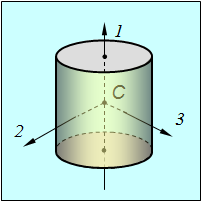
Рис. 7.15. Главные оси однородного цилиндра

У тела с центральной симметрией (например, у однородного шара) любые три взаимно перпендикулярные оси, проходящие через центр симметрии, являются главными. Для них

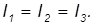
Такие тела называются шаровыми волчками. Любая ось шарового волчка, проходящая через центр симметрии, является главной (а, значит, и свободной).

В общем случае главные моменты инерции тела различны, то есть

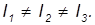
Такое тело называется асимметричным волчком. Примером асимметричного волчка может служить однородный прямоугольный параллелепипед (рис. 7.16).

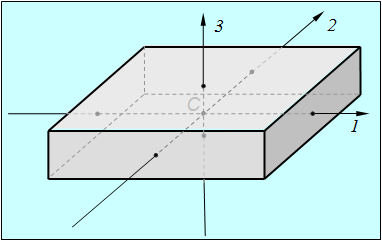
Рис. 7.16. Главные оси однородного параллелепипеда

При «почти» свободном вращении на тело могут действовать малые возмущения. Если при таких возмущениях ось вращения мало изменяет свое положение, то вращение называется устойчивым. В противном случае говорят о неустойчивом вращении.

Пусть для асимметричного волчка для определенности имеет место следующее соотношение между главными моментами инерции:

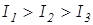
Можно показать, что вращение вокруг осей 1 и 3 (то есть осей с максимальными и минимальными моментами инерции) будет устойчивым, а вокруг оси 2 (с промежуточным по величине моментом инерции) — неустойчивым.

Видео 7.4. Устойчивость полета в воздухе прямоугольного параллелепипеда

Пусть тело вращается вокруг одной из главных осей, например, вокруг оси z. Тогда вектор угловой скорости имеет вид

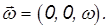
Компоненты момента импульса тела будут равны

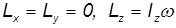
или в векторном виде

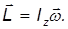
То есть этом случае момент импульса параллелен оси вращения

Видео 7.5. Устойчивое вращение стержня, диска и цепочки вокруг той свободной оси, которой соответствует максимальный момент инерции

Если тело вращается в отсутствие внешних сил (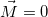), то согласно закону сохранения момента импульса в этом случае

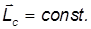
В общем случае вектор угловой скорости вращается вокруг момента импульса. Однако если ось вращения совпадает с одной из главных осей, то ось вращения сохраняет свою ориентацию в пространстве в отсутствие внешних сил.