7.3. Плоское движение твердого тела
Рассмотрим теперь плоское движение твердого тела, то есть движение, при котором точки тела описывают траектории, лежащие в параллельных плоскостях. Пример такого движения — вращение колеса автомобиля при его движении по прямой. Можно взять любую точку 0 тела и мысленно провести через нее ось вращения перпендикулярно плоскостям, в которых лежат траектории точек тела. Тогда ось вращения будет двигаться поступательно, оставаясь все время параллельной самой себе.
Видео 7.2. Плоское движение твердого тела в однородном поле тяжести. Полет плоской картонной фигуры
Соответственно, скорость 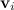 элементарной массы
элементарной массы 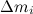 твердого тела складывается из скорости
твердого тела складывается из скорости 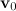 поступательного движения точки 0 и линейной скорости вращения вокруг связанной с ней (мысленно проведенной) оси:
поступательного движения точки 0 и линейной скорости вращения вокруг связанной с ней (мысленно проведенной) оси:
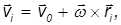
где 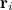 — радиус-вектор, определяющий положение элементарной массы по отношению к точке 0.
— радиус-вектор, определяющий положение элементарной массы по отношению к точке 0.
Кинетическая энергия элементарной массы равна тогда:
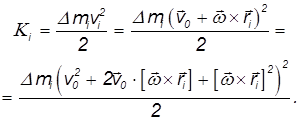
Векторное произведение
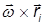
имеет модуль, равный 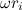 , где
, где 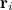 — расстояние массы
— расстояние массы 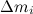 от оси вращения. Следовательно, третье слагаемое в скобках равно
от оси вращения. Следовательно, третье слагаемое в скобках равно 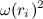 . Второе слагаемое, представляющее собой смешанное произведение векторов, не меняется при циклической перестановке сомножителей:
. Второе слагаемое, представляющее собой смешанное произведение векторов, не меняется при циклической перестановке сомножителей:
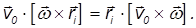
В результате получим для кинетической энергии элемента твердого тела следующее выражение
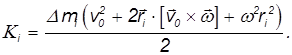
Для нахождения кинетической энергии тела просуммируем по всем элементарным массам:
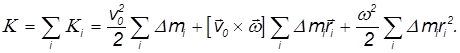
Сумма элементарных масс

есть масса твердого тела. Выражение
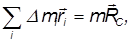
где  — радиус-вектор центра масс тела относительно точки 0.
— радиус-вектор центра масс тела относительно точки 0.
Наконец,
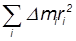
— есть момент инерции тела 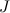 относительно оси вращения. Поэтому для кинетической энергии твердого тела можно записать формулу:
относительно оси вращения. Поэтому для кинетической энергии твердого тела можно записать формулу:
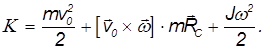
Поскольку выбор мысленной оси вращения всецело в нашей власти, мы упростим полученное выражение, взяв в качестве точки 0 центр масс тела. Тогда 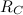 = 0 и кинетическая энергия тела при плоском движении равна
= 0 и кинетическая энергия тела при плоском движении равна
![]()
Здесь 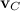 — скорость движения центра масс, a
— скорость движения центра масс, a 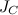 — момент инерции относительно оси, проходящей через центр масс и ортогональной плоскости, где лежат траектории точек тела. Таким образом, кинетическая энергия твердого тела при плоском движении слагается из энергии поступательного движения со скоростью, равной скорости центра масс и энергии вращения вокруг оси, проходящей через центр масс тела.
— момент инерции относительно оси, проходящей через центр масс и ортогональной плоскости, где лежат траектории точек тела. Таким образом, кинетическая энергия твердого тела при плоском движении слагается из энергии поступательного движения со скоростью, равной скорости центра масс и энергии вращения вокруг оси, проходящей через центр масс тела.
Движение твердого тела определяется действующими на тело внешними силами и моментами этих сил
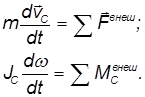
Индекс  в обозначениях для момента внешней силы означает проекцию момента на ось вращения.
в обозначениях для момента внешней силы означает проекцию момента на ось вращения.
В следующих примерах мы имеем дело с плоским движением.
Видео 7.3. Зависимость поведения цилиндров на наклонной плоскости от характера распределение массы по их объему
Пример 1. Круглое однородное тело (обруч, цилиндр, шар) радиусом 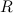 и массой
и массой 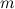 скатывается без скольжения по наклонной плоскости под углом
скатывается без скольжения по наклонной плоскости под углом 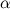 к горизонту с высоты
к горизонту с высоты 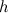 (рис. 7.12). Начальная скорость тела равна нулю. Найдем скорость центра масс каждого тела в конце спуска.
(рис. 7.12). Начальная скорость тела равна нулю. Найдем скорость центра масс каждого тела в конце спуска.

Рис. 7.12. Скатывание тела с наклонной плоскости
Рассмотрение данной задачи можно вести двумя способами.
1-й способ. По условию тело катится без проскальзывания. Это условие используется у нас дважды. Сила трения между телом и плоскостью действует в точке соприкосновения и в отсутствие скольжения не превышает своего максимального значения:
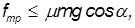
где 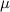 — коэффициент трения скольжения.
— коэффициент трения скольжения.
Оси координат удобно направить следующим образом: ось х — вдоль движения, ось у — перпендикулярно наклонной плоскости. Тело движется под действием трех сил: силы тяжести 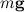 , силы трения
, силы трения 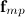 и силы нормального давления
и силы нормального давления 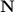 , так что уравнение поступательного движения центра инерции тела имеет вид:
, так что уравнение поступательного движения центра инерции тела имеет вид:
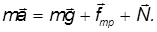
Вдоль оси у тело не движется. Проецируя уравнение движения центра масс на ось у, получаем для силы нормального давления соотношение:
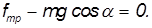
Проекция уравнения движения на ось х дает:
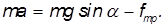
Так как линейная скорость точек соприкосновения цилиндра с наклонной плоскостью равна нулю (опять используем условие отсутствия проскальзывания), то скорость (ускорение) поступательного движения связаны с угловой скоростью (угловым ускорением) тела обычными соотношениями:
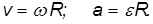
Кроме поступательного движения, тело еще и вращается. Вращение удобно описывать относительно оси z, проходящей через центр масс цилиндра.
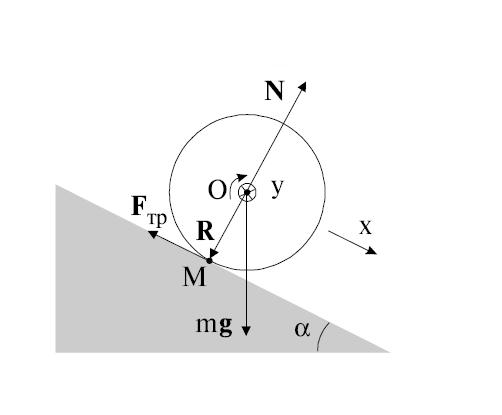
Выбор этот обусловлен тем, что линии действия силы тяжести и силы нормального давления плоскости проходят через ось вращения и, следовательно, моменты этих сил равны нулю. Таким образом, цилиндр вращается только под действием силы трения, и уравнение вращательного движения имеет вид:
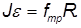
Таким образом, получается система 4-х уравнений, описывающих поступательное и вращательное движение с дополнительным неравенством, выражающим закон трения. Решая систему уравнений, находим:
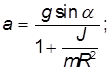
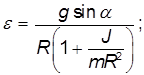
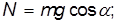
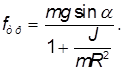
Чем больше момент инерции относительно оси, проходящей через центр масс, тем меньше ускорение тела. Мы уже получили ответ на один из вопросов задачи: шар будет двигаться быстрее цилиндра, а цилиндр — быстрее обруча. Подставляя решение для силы трения в неравенство, выражающее закон трения, находим условие, при котором будет отсутствовать проскальзывание:
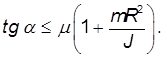
Смысл этого условия прост: наклон не должен быть слишком крут.
Итак, центр масс тела движется вдоль плоскости с постоянным ускорением a, так что зависимость пройденного пути и скорости от времени имеет вид:
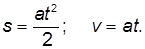
Отсюда следует связь скорости и пройденного пути:
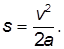
К концу спуска тело проходит путь

так что его скорость достигает величины
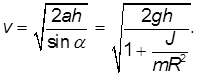
Подставляя сюда моменты инерции обруча (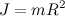 ), цилиндра (
), цилиндра (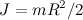 ) и шара (
) и шара (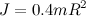 ), находим соответственно:
), находим соответственно:
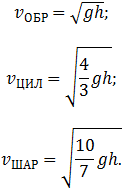
2-й способ. Используем закон сохранения полной энергии. В конце спуска тело приобретает кинетическую энергию
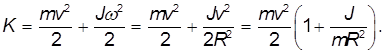
Эта кинетическая энергия приобретена за счет потенциальной энергии 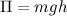 . Отсюда следует найдено выше выражение для скорости тела в конце спуска. Такой способ намного короче, но он не позволяет узнать детали процесса: действующие на тело силы и т.п.
. Отсюда следует найдено выше выражение для скорости тела в конце спуска. Такой способ намного короче, но он не позволяет узнать детали процесса: действующие на тело силы и т.п.
В рассмотренном выше примере мы считали примере мы имели дело со случаем, когда проскальзывание отсутствовало. Это позволило утверждать простую связь (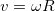 ) между угловой и линейной скоростями тела и его радиусом. Сила трения покоя находилась при этом в результате решения уравнений движения. В случае, когда тело движется с проскальзыванием, заранее известной связи между линейной и угловой скоростями нет. Зато мы заранее знаем силу трения: раз точка соприкосновения тела с поверхностью скользит по поверхности, сила трения есть сила трения скольжения,модуль которой связан с силой нормального давления законом Амонтона — Кулона.
) между угловой и линейной скоростями тела и его радиусом. Сила трения покоя находилась при этом в результате решения уравнений движения. В случае, когда тело движется с проскальзыванием, заранее известной связи между линейной и угловой скоростями нет. Зато мы заранее знаем силу трения: раз точка соприкосновения тела с поверхностью скользит по поверхности, сила трения есть сила трения скольжения,модуль которой связан с силой нормального давления законом Амонтона — Кулона.
Силы трения, как уже говорилось, направлены так, чтобы препятствовать относительному проскальзыванию соприкасающихся тел. Часто путают это возможное проскальзывание с осуществляемым поступательным движением. Необходимо четко понимать, что не редки случаи, когда сила трения не тормозит, но ускоряет тело, то есть направлена по его движению. Самый известный пример — трогание автомобиля с места. Колеса начинают вращаться и проскальзывают по земле назад. Соответственно, сила трения направлена вперед, и именно она заставляет автомобиль трогаться. Чтобы ближе познакомиться с подобными случаями, рассмотрим пример.
Пример 2. Цирковой артист бросает на арену обруч массой 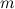 и радиусом
и радиусом 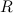 , который начинает катиться в горизонтальном направлении со скоростью
, который начинает катиться в горизонтальном направлении со скоростью 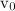 (рис. 7.13). При этом обручу придано обратное вращение с угловой скоростью
(рис. 7.13). При этом обручу придано обратное вращение с угловой скоростью 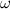 . Найдем, при какой угловой скорости обруч после остановки покатится назад к артисту, а также конечную скорость
. Найдем, при какой угловой скорости обруч после остановки покатится назад к артисту, а также конечную скорость 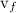 поступательного движения обруча.
поступательного движения обруча.
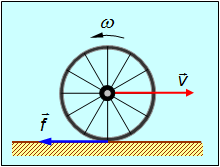
Рис. 7.13. Движение обруча с обратным вращением
При обратном вращении обруча точка его касания с ареной движется вперед как из-за вращения, так и из-за поступательного движения обруча. Поэтому неизбежно существует проскальзывание и, значит, сила трения достигает своего максимального значения. Она тормозит как поступательное движение, так и вращение обруча. Может случиться так, что поступательное движение обруча будет остановлено в тот момент, когда он еще сохраняет обратное вращение. Далее сила трения начнет ускорять обруч по направлению к артисту. Ускорение это прекратится, когда исчезнет тенденция к проскальзыванию, после чего обруч покатится назад равномерно с некоторой установившейся скоростью 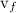 . Может, однако, случиться и так, что раньше будет остановлено обратное вращение, и тогда обруч сохранит поступательное движение вперед, изменив направление вращения на прямое. Чтобы различить эти два случая, качественных рассуждений недостаточно, и мы обратимся к формулам.
. Может, однако, случиться и так, что раньше будет остановлено обратное вращение, и тогда обруч сохранит поступательное движение вперед, изменив направление вращения на прямое. Чтобы различить эти два случая, качественных рассуждений недостаточно, и мы обратимся к формулам.
Направим ось ОХ направо (в направлении красной стрелки на рис. 7.13), ось вращения ОZ направим на нас (см. следующий пример, там эту ось удобнее направить от нас, то есть за чертеж), то есть в направлении «обратного» вращения, ось OY направим как обычно, вверх. Плоское движение обруча представим как суперпозицию его поступательного движения вместе с центром масс (геометрическим центром, поскольку обруч предполагается однородным). Спроектируем линейные и угловые скорости на соответствующие оси. Тогда, до тех пор, пока сила трения есть сила трения скольжения и направлена она налево, уравнения движения имеют вид
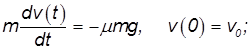
(7.3.1)

(7.3.2)
Уравнение (7.3.1) описывает движение центра масс обруча, а уравнение (7.3.2) его вращение вокруг оси проходящей через центр масс в той системе отсчета, в которой она покоится (системе центра масс). В (7.3.2) учтено, что момент инерции однородного обруча относительно его оси симметрии равен 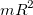 . После элементарного интегрирования получаем
. После элементарного интегрирования получаем
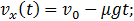
(7.3.3)
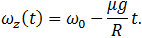
(7.3.4)
Поступательное движение прекратится, то есть 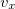 станет равным нулю, в момент времени
станет равным нулю, в момент времени
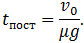
(7.3.5)
Вращение прекратится, то есть 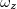 станет равным нулю,в момент времени
станет равным нулю,в момент времени
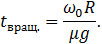
(7.3.6)
Их отношение
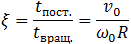
(7.3.7)
может быть любым ввиду независимости начальных скоростей поступательного 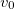 и вращательного
и вращательного 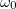 движений.
движений.
Для дальнейшего анализа введем в рассмотрение скорость 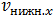 нижней точки обруча — той его точки, которая касается поверхности арены. Отметим уже здесь, что условием исчезновения проскальзывания является обращение в ноль скорости именно этой точки, потому что скорость соответствующей точки на поверхности арены (той, которой касается обруч) очевидным образом в нашей системе отсчета, где арена неподвижна, равна нулю. Отсутствие проскальзывания это и есть неподвижность этих двух точек относительно друг друга. При выбранном направлении осей OZ и OX, имеем
нижней точки обруча — той его точки, которая касается поверхности арены. Отметим уже здесь, что условием исчезновения проскальзывания является обращение в ноль скорости именно этой точки, потому что скорость соответствующей точки на поверхности арены (той, которой касается обруч) очевидным образом в нашей системе отсчета, где арена неподвижна, равна нулю. Отсутствие проскальзывания это и есть неподвижность этих двух точек относительно друг друга. При выбранном направлении осей OZ и OX, имеем
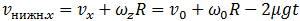
(7.3.8)
Если 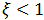 , то первым прекратится поступательное движение обруча. В момент времени
, то первым прекратится поступательное движение обруча. В момент времени 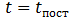 скорости (7.3.3) и (7.3.8) будут иметь значения
скорости (7.3.3) и (7.3.8) будут иметь значения
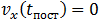
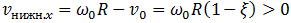
Нижняя точка обруча, за счет продолжающегося вращения, будет по-прежнему скользить относительно арены направо (направо на рисунке 7.13), сила трения скольжения сохранит свою величину и направление налево. Соответственно, центр обруча начнет ускорятся налево, то есть 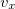 станет меньше нуля и начнет расти по модулю, вращение против часовой стрелки (на рисунке 7.13) будет продолжать замедлятся. Другими словами, при
станет меньше нуля и начнет расти по модулю, вращение против часовой стрелки (на рисунке 7.13) будет продолжать замедлятся. Другими словами, при 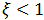 обруч в момент времени (7.3.5) начинает возвращаться к бросившему его артисту.
обруч в момент времени (7.3.5) начинает возвращаться к бросившему его артисту.
Как следует из (7.3.8), в момент времени
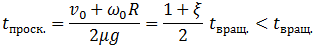
(7.3.9)
скорость нижней точки обруча 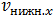 из (7.3.8) обращается в ноль, проскальзывание прекращается, сила трения скольжения скачком сменяется равной нулю силой трения покоя (силой трения качения пренебрегаем) и обруч начинает катится к артисту с постоянной скоростью движения центра масс
из (7.3.8) обращается в ноль, проскальзывание прекращается, сила трения скольжения скачком сменяется равной нулю силой трения покоя (силой трения качения пренебрегаем) и обруч начинает катится к артисту с постоянной скоростью движения центра масс
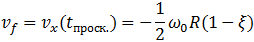
(7.3.10)
вращаясь против часовой стрелки с постоянной угловой скоростью
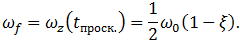
(7.3.11)
Если 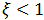 , то первым, в момент времени (7.3.6), прекратится вращение обруча. В момент времени
, то первым, в момент времени (7.3.6), прекратится вращение обруча. В момент времени 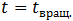 скорость (7.3.8) нижней точки обруча будет равна скорости его центра и положительна:
скорость (7.3.8) нижней точки обруча будет равна скорости его центра и положительна:
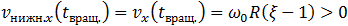
(7.3.12)
Скольжение остается, сила трения скольжения сохраняет свою величину и направление налево, но обруч под действием этой силы трения скольжения начинает вращаться по часовой стрелке (напоминаем: налево, направо, по или против часовой стрелки — на рисунке 10). В результате этого скорость центра масс (центра обруча) будет уменьшаться, скорость вращения увеличиваться, в момент времени
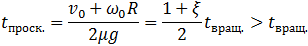
(7.3.13)
проскальзывание обруча прекратится и обруч начнет равномерно удаляться от артиста со скоростью центра (7.3.10) и угловой скоростью вращения (7.3.11). Напомним, что в этом случае  , так что
, так что 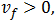 а
а 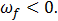
Таким образом, ответ на вопрос: "Вернется обруч или укатится?" определяется начальными условиями, а конкретнее величиной параметра 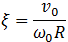 , который имеет простой физический смысл: это отношение модуля
, который имеет простой физический смысл: это отношение модуля
скорости любой точки обруча за счет его поступательного движения вместе с центром масс к модулю скорости той же точки за счет вращения обруча вокруг оси, проходящей через его центр масс, в начальный момент времени.
Пример 3. Описать движение обруча (см. предыдущий пример), если ему придано прямое вращение (рис. 7.14). Поскольку обруч вращается теперь на рис. 7.14 по часовой стрелке, направим ось вращения OZ от нас, то есть за чертеж — в отличие от предыдущего случая.
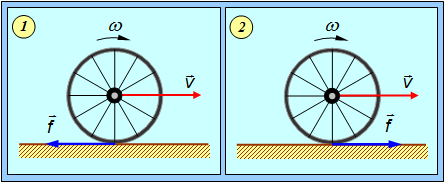
Рис. 7.14. Движение обруча с прямым вращением: 1 – 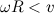 ; 2 –
; 2 – 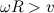
Начальная скорость нижней точки обруча складывается из скорости поступательного движения 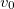 и линейной скорости
и линейной скорости 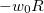 за счет вращения, направленной в противоположную сторону. В связи с этим надо различать два случая.
за счет вращения, направленной в противоположную сторону. В связи с этим надо различать два случая.
1 случай  или
или 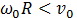 . Тогда начальная скорость
. Тогда начальная скорость 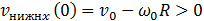 нижней точки обода положительна, то есть, направлена в ту же сторону, что и скорость
нижней точки обода положительна, то есть, направлена в ту же сторону, что и скорость 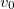 . Значит, сила трения f направлена в противоположную сторону, как показано на рис. 11–1. В связи с изменением положительного направления оси вращения необходимо лишь изменить знак перед вторым слагаемым в уравнении (7.3.4). Решение уравнений движения в рассматриваемом случае имеют вид
. Значит, сила трения f направлена в противоположную сторону, как показано на рис. 11–1. В связи с изменением положительного направления оси вращения необходимо лишь изменить знак перед вторым слагаемым в уравнении (7.3.4). Решение уравнений движения в рассматриваемом случае имеют вид
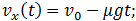
(7.3.14)
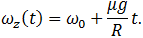
(7.3.15)
При новом выборе направления оси вращения скорость нижней точки обруча записывается в виде
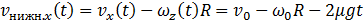
(7.3.16)
Момент 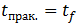 исчезновения проскальзывания определится из того же соотношения равенства нулю скорости нижней точки обруча или равенства по модулю противоположно направленных скоростей этой точки за счет поступательного движения вместе с центром масс и вращательного движение вокруг оси, проходящей через центр масс:
исчезновения проскальзывания определится из того же соотношения равенства нулю скорости нижней точки обруча или равенства по модулю противоположно направленных скоростей этой точки за счет поступательного движения вместе с центром масс и вращательного движение вокруг оси, проходящей через центр масс:
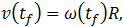
откуда находим:
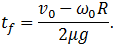
Скорость поступательного движения обруча в этот момент становится равной
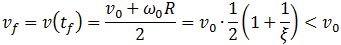
и остается потом неизменной. Эта скорость меньше начальной скорости поступательного движения обруча.
2 случай 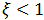 или
или 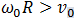 . В этом случае скорость нижней точки обода отрицательна, направлена против скорости
. В этом случае скорость нижней точки обода отрицательна, направлена против скорости 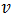 . Значит, сила трения
. Значит, сила трения 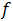 направлена по
направлена по 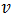 (см. рис.11-2).
(см. рис.11-2).
Соответственно, в уравнениях движения и их решениях (7.3.14) и (7.3.15) надо изменить знаки на противоположные перед вторыми слагаемыми, содержащими изменившую направление силу трения, получаем:
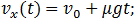
(7.3.17)
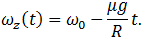
(7.3.18)
Соответственно, выражение для скорости нижней точки обруча приобретает вид:
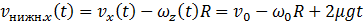
(7.3.19)
Момент прекращения проскальзывания 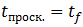 определяется аналогично и оказывается равным:
определяется аналогично и оказывается равным:
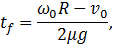
а для скорости установившегося движения получается вновь выражение
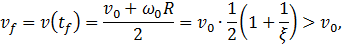
но в данном случае она будет больше (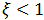 ) начальной скорости поступательного движения.
) начальной скорости поступательного движения.
Объединяя оба случая в один, записываем окончательный результат:
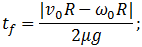
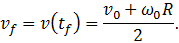
Дополнительная информация
http://www.plib.ru/library/book/14978.html Сивухин Д.В. Общий курс физики, том 1, Механика Изд. Наука 1979 г. — стр. 256 (§ 48, задача 9): рассмотрено движение маятника Максвелла, включая силу натяжения нитей подвеса в нижней точке.
http://kvant.mirror1.mccme.ru/pdf/1997/04/kv0497khorozov.pdf — журнал «Квант» — решение задачи об отскоке вращающегося мяча от плоской стенки (С. Хорозов).
http://kvant.mirror1.mccme.ru/pdf/1998/04/kv0498chernoutsan.pdf — журнал «Квант» — применение законов динамики твердого тела в задаче о падении вертикальной палочки на горизонтальный стол (А. Черноуцан).
http://kvant.mirror1.mccme.ru/pdf/1999/02/kv0299chernoutsan.pdf — журнал «Квант» — продолжение задачи о падении вертикальной палочки на горизонтальный стол (А. Черноуцан).



