8.3. Центробежная сила инерции
Представим себе диск, равномерно вращающийся с угловой скоростью ![]() . Вместе с диском вращается надетый на спицу шарик, соединенный с центром диска пружиной (рис. 8.3).
. Вместе с диском вращается надетый на спицу шарик, соединенный с центром диска пружиной (рис. 8.3).

Рис. 8.3. Центробежная сила инерции в системе отсчета, связанной с вращающимся диском
Шарик покоится относительно диска и занимает на спице такое положение, при котором сила натяжения пружины ![]() оказывается равной произведению массы шарика
оказывается равной произведению массы шарика ![]() на нормальное (центростремительное) ускорение (при равномерном вращении диска тангенциальное ускорение шарика, очевидным образом, равно нулю)
на нормальное (центростремительное) ускорение (при равномерном вращении диска тангенциальное ускорение шарика, очевидным образом, равно нулю)
![]()
где 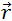 — радиус-вектор, проведенный к шарику из центра диска (см. рис. 8.3). Но так рассуждает наблюдатель, смотрящий на вращение диска из инерциальной системы отсчета. Свяжем с диском вращающуюся неинерциальную систему отсчета К', в которой диск вместе с шариком покоится. Условие равновесия шарика в этой системе имеет вид:
— радиус-вектор, проведенный к шарику из центра диска (см. рис. 8.3). Но так рассуждает наблюдатель, смотрящий на вращение диска из инерциальной системы отсчета. Свяжем с диском вращающуюся неинерциальную систему отсчета К', в которой диск вместе с шариком покоится. Условие равновесия шарика в этой системе имеет вид:
![]()
Наблюдатель во вращающейся системе отсчета объясняет равновесие шарика наличием силы инерции
![]()
направленной от центра диска 0' по радиус-вектору 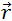 .
.
Сила инерции, действующая на материальную точку в равномерно вращающейся с угловой скоростью ω системе отсчета, называется центробежной силой инерции:
![]()
Здесь ![]() — вектор, проведенный к материальной точке от оси вращения ортогонально последней. Мы ввели его, чтобы отличить от радиус-вектора
— вектор, проведенный к материальной точке от оси вращения ортогонально последней. Мы ввели его, чтобы отличить от радиус-вектора ![]() в том случае, когда начало координат лежит на оси вращения, но не в плоскости вращения материальной точки.
в том случае, когда начало координат лежит на оси вращения, но не в плоскости вращения материальной точки.
Видео 8.4. Центробежная сила инерции: подвешенные шарики
При произвольном положении начала отсчета на оси вращения, радиус-вектор некоторой материальной точки всегда можно представить в виде
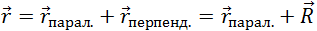
где 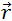 парал.— параллельная оси вращения, более того, лежащая на оси вращения (напомним: начинается вектор
парал.— параллельная оси вращения, более того, лежащая на оси вращения (напомним: начинается вектор 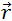 на оси вращения) составляющая радиус вектора
на оси вращения) составляющая радиус вектора 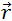 , а
, а 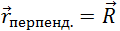 — перпендикулярная к оси вращения его составляющая, начинающаяся на оси вращения, в центре той окружности, по которой движется рассматриваемая точка. С помощью известной формулы
— перпендикулярная к оси вращения его составляющая, начинающаяся на оси вращения, в центре той окружности, по которой движется рассматриваемая точка. С помощью известной формулы
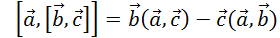
учитывая, что векторное произведение 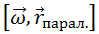 и скалярное произведение
и скалярное произведение 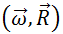 равны нулю всегда, можно показать, что выражение для центробежной силы инерции представляется в виде
равны нулю всегда, можно показать, что выражение для центробежной силы инерции представляется в виде
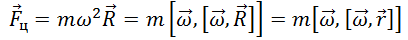
Таким образом, в общем случае, при произвольном выборе начала отсчета на оси вращения, для любого положения материальной точки, действующую на неё центробежную силу инерции, можно записать в виде
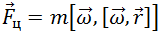
Видео 8.5. «Поразительное» поведение цепи — и здесь не обошлось без центробежной силы инерции. Цепь легкая, почти без трения между звеньями
Видео 8.6. «Поразительное» поведение цепи 2. Цепь тяжелая, с большим трением между звеньями
Пример. Сосуд с жидкостью вращается с угловой скоростью ![]() вокруг вертикальной оси (рис. 8.4). Найдем форму поверхности жидкости.
вокруг вертикальной оси (рис. 8.4). Найдем форму поверхности жидкости.
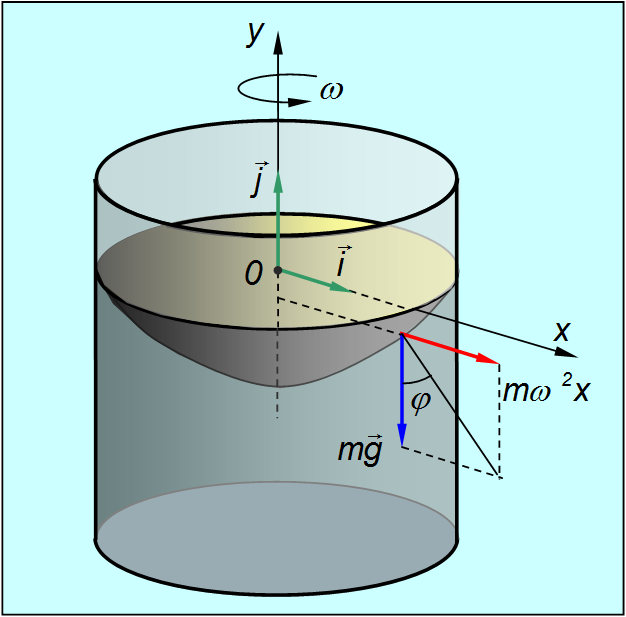
Рис. 8.4. Форма поверхности вращающейся жидкости
Задачу решаем в системе отсчета, вращающейся вместе с жидкостью. В этой системе жидкость неподвижна, но кроме силы тяжести на нее действует центробежная сила инерции. Поверхность жидкости симметрична относительно оси вращения. Рассмотрим сечение этой поверхности какой-нибудь вертикальной плоскостью, содержащей ось вращения, которую мы примем за ось ![]() .
.
Возьмем на поверхности элемент жидкости массой ![]() , расположенный в точке с координатой
, расположенный в точке с координатой ![]() . На него действует сила тяжести
. На него действует сила тяжести ![]() и центробежная сила инерции
и центробежная сила инерции ![]() (здесь координата
(здесь координата ![]() есть расстояние от оси вращения, а
есть расстояние от оси вращения, а ![]() и
и ![]() — единичные орты). Результирующая этих сил наклонена к вертикали под углом
— единичные орты). Результирующая этих сил наклонена к вертикали под углом ![]() таким, что
таким, что
![]()
Поверхность жидкости, описываемая функцией ![]() , всегда располагается ортогонально линии действия внешних сил. Как известно, тангенс того же угла можно найти как отношение приращений
, всегда располагается ортогонально линии действия внешних сил. Как известно, тангенс того же угла можно найти как отношение приращений
![]()
то есть как производную. Получаем уравнение
![]()
которое легко интегрируется:
![]()
Это уравнение, как известно, описывает параболу. Вращение этой параболы задает параболоид вращения. Таким образом, поверхность вращающейся жидкости принимает форму параболоида вращения. При ![]() имеем
имеем ![]() , то есть плоскую горизонтальную поверхность.
, то есть плоскую горизонтальную поверхность.
Видео 8.7. Циркулярная «пила» из бумаги – неожиданное применение центробежной силы инерции
Видео 8.8. Сила Кориолиса: траектория движения шарика по вращающейся платформе
Дополнительная информация
http://www.plib.ru/library/book/14978.html — Сивухин Д.В. Общий курс физики, том 1, Механика Изд. Наука 1979 г.–— стр.349–353 (§66): детально обсуждается вес тел и проблема взвешивания на Земле.



