9.1. Закон Паскаля

Утверждение, известное как закон Паскаля или закон гидростатики, но в равной мере справедливое и для газов, гласит:

Данное свойство жидкости можно продемонстрировать с помощью прибора, называемого шаром Паскаля (рис. 9.1).

Рис. 9.1. Шар Паскаля

Проведем мысленно в некотором объеме жидкости, находящемся в равновесии, площадку 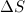. Отдельные частицы жидкости действуют друг на друга и, в частности, на площадку 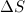с силой, зависящей от степени сжатия. Это воздействие характеризуется давлением

где 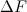— равнодействующая всех сил, с которыми жидкость действует на площадку.

Один паскаль — давление, производимое силой один ньютон, равномерно распределенной по нормальной к ней поверхности площадью 1 м².

Например, если булавка вдавливается в поверхность стола силой 10 Н, а площадь её острия 0,05 мм², то давление булавки на стол равно

На рис. 9.2 показаны характерные масштабы давлений, встречающихся в природе.

Рис. 9.2. Масштабы давлений, встречающихся в окружающем мире

Обратим внимание: давление — скалярная величина, для него неприменимо понятие направления. Сила же, с которой жидкость давит на элементарную площадку 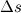, всегда направлена по нормали к площадке.

Если внутри жидкости поместить тонкую пластинку площадью S, то со стороны жидкости на нее будет действовать сила давления, перпендикулярная к её поверхности (рис. 9.3).

Рис. 9.3. Сила давления в жидкости

Действительно, если бы сила была направлена не под прямым углом к выбранной площадке, то её касательная составляющая из-за отсутствия сопротивления сдвигу привела бы жидкость в движение, что противоречит условию неподвижности.

Одно из проявлений закона Паскаля можно наблюдать в гидравлическом прессе (рис. 9.4).

Рис. 9.4. Принцип работы гидравлического пресса

Два сообщающихся сосуда заполнены жидкостью и закрыты поршнями различной площади. По закону Паскаля, давления под поршнями одинаковы p₁ = p₂, то есть

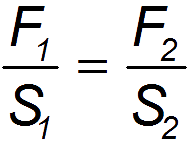
или

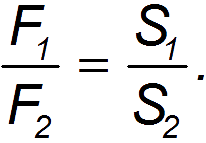
Таким образом, сила давления второго поршня больше силы давления первого во столько раз, во сколько площадь второго поршня больше площади первого. Гидравлический пресс — простой механизм, позволяющий развивать колоссальные силы, используемые для прессования различных изделий из металлов и пластмасс. Обозначим h₁ и h₂ — ходы поршней. Вследствие практической несжимаемости объёмы жидкости, перешедшей из одного цилиндра в другой, одинаковы:

Работы, совершаемые силами F₁₍₂₎ за один ход, вычисляются как

и

так что их отношение будет

Как и следовало ожидать, пресс дает выигрыш в силе, но не в совершаемой работе.

На том же принципе основано устройство гидравлического подъёмника (рис. 9.5). Обратите внимание на то, что площадь поперечного сечения первого цилиндра, в котором возвратно-поступательно движется поршень, накачивающий масло, значительно меньше площади поперечного сечения цилиндра, который направляет движение второго поршня. Второй поршень передает усилие на шток, соединённый жёстко с платформой, на которой поднимается груз — автомобиль. При одинаковом давлении масла в системе силы давления, с которыми масло действует на поршни, значительно отличаются.

Открывание вентиля 3 приводит к тому, что под действием давления масло перетекает в бак для его хранения.

Рис. 9.5. Работа гидравлического подъёмника

Определим давление внутри жидкости, считая её несжимаемой, то есть считая её плотность неизменной независимо от глубины. Пусть на жидкость в сосуде действует внешнее давление p₀. Выделим мысленно в жидкости вертикальный цилиндр с поперечным сечением S и высотой h (рис. 9.6).

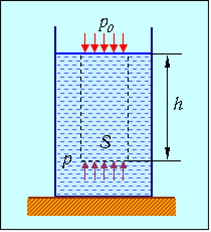
Рис. 9.6. Давление жидкости в поле сил тяжести

На верхний слой жидкости действует внешнее давление p₀, которое также передается и другим слоям жидкости. К этому давлению в нижележащих слоях добавляется давление, создаваемое весом сло`в жидкости, расположенных выше. На верхнее основание цилиндра действует сила F₀ = p₀S, на нижнее основание F = pS, где p — давление на глубине h. Кроме того, вертикально вниз действует сила тяжести столба жидкости, находящейся в объёме цилиндра:

где ρ — плотность жидкости, hS — её объём.

Запишем условие равновесия выделенного столба жидкости:

или

Следовательно, давление в жидкости на глубине h будет равно

где ρgh — гидростатическое давление жидкости, обусловленное ее тяжестью.

Согласно полученной формуле, сила давления на нижние слои жидкости будет больше, чем на верхние. Поэтому на тело, погруженное в жидкость, действует выталкивающая сила, называемая силой Архимеда. Погрузим в жидкость на глубину h параллелепипед с площадью основания S и высотой ребра a (рис. 9.7).

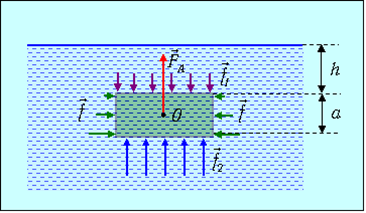
Рис. 9.7. Сила Архимеда, действующая на тело, погружённое в однородную жидкость

Давление на глубине h равно

и потому на верхнее основание действует сила

На глубине h+a давление равно

и потому на нижнее основание действует сила

Равнодействующая этих двух сил направлена вверх и равна по величине

Здесь Sa = V — объём погружённой части тела, m = pV — жидкости (газа) того же объёма.

Полученное уравнение представляет математическую формулировку закона Архимеда:

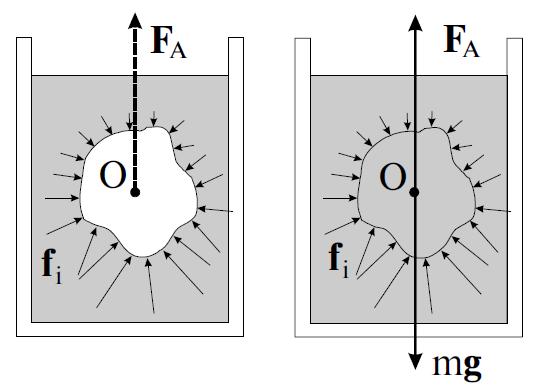
Рис. 9.8. Иллюстрация закона Архимеда

Дополнительная информация

http://www.plib.ru/library/book/14978.html — Сивухин Д.В. Общий курс физики, том 1, Механика. Изд. Наука 1979 г. — стр. 448–455 (§91): гидростатика, закон Архимеда, условия устойчивого равновесия плавающих тел, решение задач.

http://kvant.mirror1.mccme.ru/1996/03/vsplyvayushchij_vozdushnyj_puz.html — Журнал «Квант» — применение второго закона Ньютона к движению всплывающих пузырьков газа (Г.Коткин).