9.2. Уравнение непрерывности

Рассмотрим теперь движение жидкости. Самый простой случай — так называемое стационарное течение. Нет никакого противоречия в употреблении слова «стационарный» рядом со словом «течение», которое подразумевает движение элементов жидкости.

Элементы жидкости приходят и уходят, но в данной точке каждый вновь пришедший элемент приобретает ту скорость, которая этой точке соответствует. Поэтому стационарное течение можно характеризовать полем скоростей, задавая векторную функцию v(r) от пространственных координат. Графически поле скоростей изображается с помощью линий тока.

На рис. 9.9 показана линия тока в области течения жидкости.

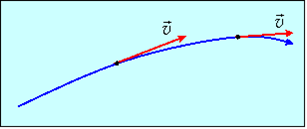
Рис. 9.9. Линия тока

Если вспомнить то, что мы знаем из школьного курса физики об электричестве, то можно сказать, что линии тока — это аналог силовых линий.

Условимся проводить линии тока так, чтобы густота их (которая характеризуется отношением числа линий 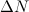к величине перпендикулярной к ним площади 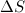, через которую они проходят) была пропорциональна величине скорости в данном месте. Часть жидкости, ограниченную линиями тока, называют трубкой тока. Для стационарного течения форма и расположение линий тока со временем не изменяются.

Рассмотрим какую-либо трубку тока. Всюду далее полагаем площадь сечения трубки достаточно малой, так что можно считать скорость жидкости одинаковой во всех точках сечения. За время dt через произвольное её сечение S проходит объём жидкости Svdt (рис. 9.10–1).

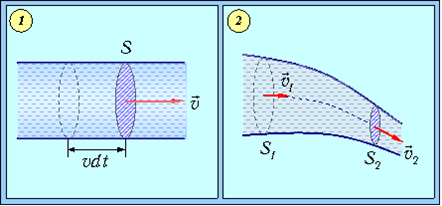
Рис. 9.10 Трубки тока

Выберем два её сечения S₁ и S₂ (рис. 9–2). За время dt через сечение S₁ пройдет объём жидкости S₁v₁dt, где v₁ — скорость течения жидкости в точках сечения S₁. Аналогично, через сечение S₂ за то же время dt пройдёт объём жидкости S₂v₂dt, где v₂ — скорость течения жидкости в точках сечения S₂. Из условия несжимаемости жидкости следует равенство объёмов жидкости, вошедших в область между сечениями S₁, S₂ и вышедших из него:

Следовательно,

Это соотношение — одна из форм теоремы о непрерывности струи. Данная теорема выражает собой факт несжимаемости жидкости.

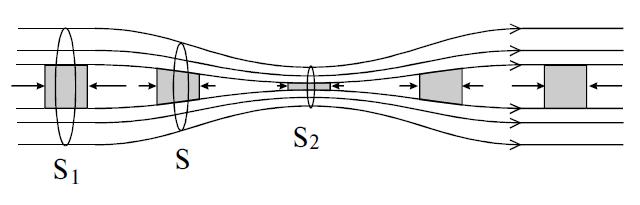
Рис. 9.11. Скорость струи в различных сечениях трубки

Теорема о непрерывности струи применима к реальным жидкостям, а также к газам, в том случае, если сжимаемостью их можно пренебречь. Прямое следствие теоремы — широко известный факт: в месте сужения трубы скорость потока возрастает. Более того, аналогичная теорема есть и в теории электромагнетизма, и там она связана с сохранением электрического заряда.

Пример. Оценим пропускную способность одного ряда участка автомагистрали. Учтём, что «Правила дорожного движения» рекомендуют держать дистанцию L между автомобилями, которая в метрах численно равна половине скорости движения, выраженной в км/час.

В этой задаче мы в сущности тоже имеем дело с уравнением непрерывности — при отсутствии «пробки» на дороге через каждое её сечение должно проходить одинаковое количество автомобилей. Поток автомобилей равен

где v — средняя скорость движения, а ρ — линейная «плотность» автомобилей на дороге, то есть число машин на единицу длины. Если l — средняя длина автомобиля, a L — средняя дистанция между ними, то

Рекомендацию «Правил дорожного движения» математически можно выразить в виде формулы:

где

— «коэффициент безопасности». В итоге приходим к выражению:

Для численной оценки примем l = 3 м, a v = 60 км/час = 16,67 м/с (допустимая скорость движения в городах). Получаем тогда:

то есть каждый ряд способен пропустить 30 машин в минуту.

При повышении скорости движения до v = 90 км/час = 25 м/с пропускная способность возрастает совершенно незначительно: в этом случае находим

Даже в пределе бесконечно большой скорости движения

предельное значение потока

При снижении скорости движения, скажем, до v = 30 км/час = 8,33 м/с пропускная способность станет

Гораздо более «эффективным» является несоблюдение дистанции. Скажем, при дистанции L, равной длине l корпуса автомобиля, и скорости движения v = 30 км/час, получаем для потока:

Но вряд ли повышение пропускной способности магистрали даже в три раза должно достигаться за счет уменьшения безопасности движения.