9.3. Уравнение Бернулли

При течении жидкости ее отдельные слои в общем случае текут с разными скоростями, скользят друг относительно друга, вследствие чего между ними возникают силы трения. Эти силы называют силами внутреннего трения. Они возникают не только в жидкостях, но и в газах.

Выделим в стационарно текущей идеальной жидкости трубку тока, ограниченную сечениям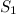и и 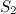, по которой слева направо течет жидкость (рис. 9.12). Пусть в месте сечения 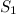заданы: скорость течения 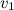, давление и высота 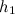, на которой расположено это сечение. Аналогично, в месте сечения 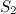заданы скорость течения 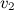, давление 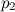и высота .

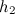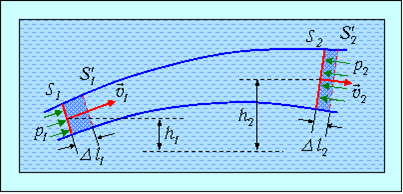
Рис. 9.12. К выводу уравнения Бернулли

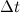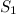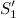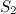За время объём жидкости переместится вдоль трубки тока, причем сечение переместится в положение , пройдя путь , сечение переместится в положение 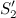, пройдя путь 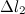. В силу уравнения непрерывности струи заштрихованные объёмы будут иметь одинаковую величину: .

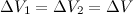Энергия каждой частицы жидкости слагается из её кинетической энергии и потенциальной энергии в поле сил тяжести. Полная энергия потока, протекающего за время 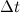через сечение 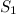, равна

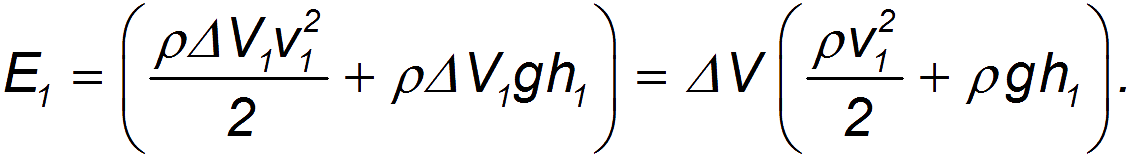
Аналогичное выражение для энергии потока имеем для сечения :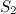

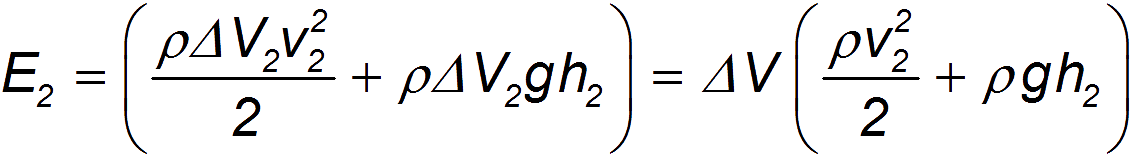
При стационарном течении между сечениями и энергия не накапливается. В идеальной жидкости силы трения отсутствуют, так что механическая энергия никуда не исчезает. Следовательно, изменение полной энергии жидкости равно работе, совершенной внешними силами

Силы давления на боковую поверхность трубки тока перпендикулярны в каждой точке к направлению перемещения частиц, вследствие чего работы не совершают. Отлична от нуля лишь работа сил давления, приложенных к сечениям 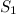и 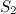. Эта работа равна

Приравнивая изменение энергии потока 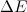работе сил давления 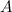, находим:

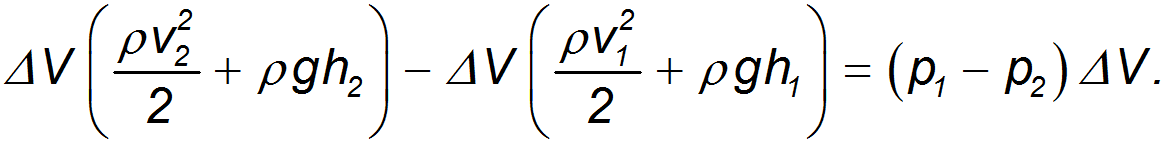
Сократив на и перенеся члены с одинаковыми индексами в одну часть равенства, получаем:

Сечения и были взяты совершенно произвольно. Поэтому можно утверждать, что

Полученное нами соотношение называется уравнением Бернулли. Это уравнение выражает собой закон сохранения механической энергии при стационарном течении несжимаемой идеальной жидкости.

В частном случае горизонтального течения жидкости 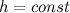уравнение Бернулли принимает вид

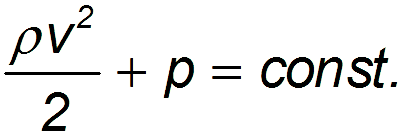
Из уравнения непрерывности

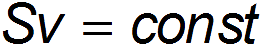
следует, что в месте сужения потока его скорость возрастает, а из уравнения Бернулли — что в этом месте падает давление.

Рис. 9.13. Скорости жидкости и давление в зависимости от сечения трубки

Когда идущие параллельными курсами корабли находятся слишком близко друг к другу, давление между ними падает и давление внешнего потока их сближает, и может привести к столкновению судов.

Пример. В сосуде проделано небольшое отверстие. Высота жидкости над отверстием равна 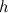. Найдем скорость вытекающей струи.

Применим уравнение Бернулли. В качестве сечения 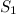возьмем поверхность жидкости, а за сечение 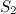примем проделанное отверстие. Давления в обоих сечениях можно считать постоянными (и равными атмосферному). Скоростью жидкости в сечении 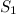можно пренебречь (если площадь сосуда много больше площади отверстия: 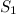>> 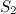) Тогда имеем:

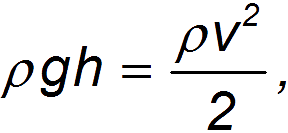
где 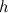— высота сечения 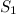над сечением 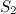(то есть уровень жидкости над отверстием), a — скорость истечения жидкости из отверстия. Получаем в итоге:

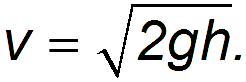
Указанное соотношение называется формулой Торричелли. Заметим, что скорость истечения струи равна скорости свободного падения тела с той же высоты. Это не удивительно, так как в основе обоих результатов лежит закон сохранения энергии при движении в однородном поле сил тяжести.

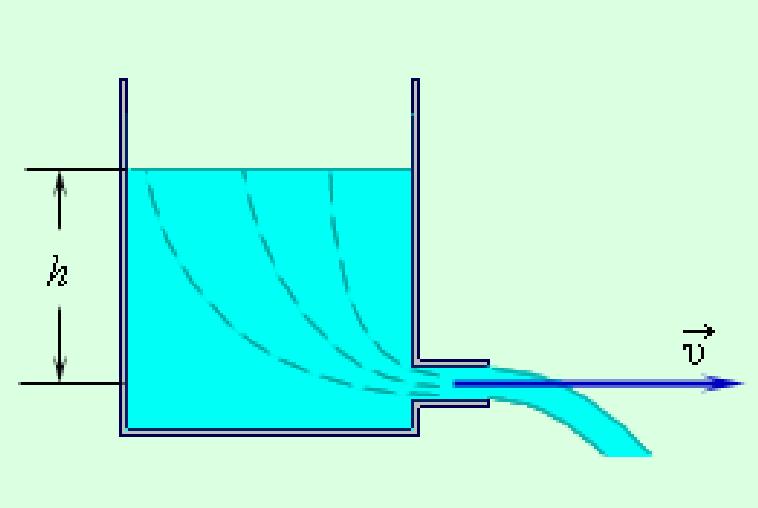
Рис. 9.14. Истечение жидкости из отверстия

Выводя уравнение Бернулли, мы пренебрегли сжимаемостью жидкости. Что касается газов, их сжимаемость намного больше, чем у жидкостей. Получим оценку применимости уравнения Бернулли к течению газов. Величина 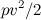, называемая динамическим давлением, должна быть мала по сравнению со статическим давлением 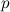. Тогда колебания давления вследствие течения газа будут невелики и его сжимаемостью можно пренебречь. Следовательно, критерием применимости уравнения Бернулли к газам служит неравенство

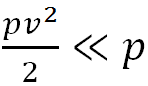
или

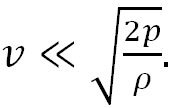
Приведем численную оценку. При нормальных условиях давление воздуха приблизительно равно 10⁵ Па, а плотность воздуха 1,29 кг/м³. Отсюда

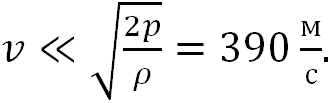
Это число близко к скорости звука и отличается от неё только коэффициентом 2 под знаком корня: в выражении для скорости звука под знаком корня стоит показатель адиабаты 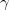, равный для воздуха при комнатных температурах 1,4. Как будет видно позже, это не случайно, поэтому критерий применимости к газу приближения «несжимаемой жидкости», в котором он считается несжимаемым, можно сформулировать так. Можно пренебречь сжимаемостью газа при скоростях его течения много меньших скорости звука в этом газе:

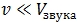
При таких скоростях мы можем применять уравнение Бернулли к газам с тем же успехом, что и к жидкостям.