9.4. Движение тел в среде с сопротивлением
Со времен опытов Галилея на Пизанской башне известно, что все тела падают в поле силы тяжести с одинаковым ускорением g.
Однако каждодневная практика указывает на другое: легкое перышко падает медленнее тяжелого металлического шарика. Понятна и причина этого — сопротивление воздуха.
Уравнения движения. Если ограничиться случаем поступательного движения невращающихся тел в неподвижной среде с сопротивлением, то сила сопротивления будет направлена против скорости. В векторном виде ее можно записать как
где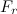 
— абсолютная величина этой силы, a 
— модуль скорости тела. Учет сопротивления среды меняет вид уравнений движения тела, брошенного под углом к горизонту:
В приведенных уравнениях учтена также выталкивающая сила Архимеда, действующая на тело: ускорение свободного падения g заменено на меньшую величину
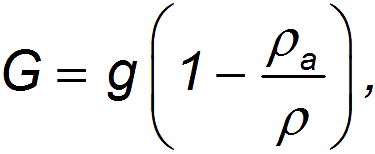
где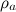 
— плотность среды (для воздуха 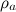= 1.29 кг/м3), а 
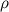— средняя плотность тела.
Действительно, вес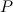 
тела в среде уменьшается на величину выталкивающей силы Архимеда
Выражая объём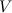 
тела через его среднюю плотность
приходим к выражению
При наличии сопротивления воздуха скорость падающего тела не может расти безгранично. В пределе она стремится к некоторому установившемуся значению, которое зависит от характеристик тела. Если тело достигло установившейся скорости падения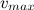 
, то из уравнений движения следует, что сила сопротивления равна весу тела (с учётом архимедовой силы):
Сила сопротивления 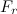как мы вскоре убедимся, есть функция скорости падения. Стало быть, полученное выражение для силы сопротивления представляет собой уравнение для определения установившейся скорости падения 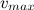. Ясно, что при наличии среды энергия тела частично расходуется на преодоление её сопротивления.
Число Рейнольдса. Разумеется, уравнения движения тела в жидкости невозможно даже начать решать, пока нам ничего неизвестно о модуле 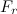силы сопротивления. Величина этой силы существенно зависит от характера обтекания тела встречным потоком газа (или жидкости). При малых скоростях этот поток является ламинарным (то есть слоистым). Его можно представить себе как относительное движение не смешивающихся между собой слоев среды.
Ламинарное течение жидкости демонстрируется на опыте, показанном на рис. 13.
Как уже отмечалось в главе 9.3, при относительном движении слоёв жидкости или газа между этими слоями возникают силы сопротивления движению, которые называются силами внутреннего трения. Эти силы обусловлены особым свойством текучих тел — вязкостью, которая характеризуется численно коэффициентом вязкости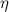 
. Приведем характерные значения 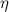для различных веществ: для воздуха ( 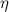= 1,8·10-5 Па·с), воды ( 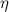= 10–3 Па·с), глицерина ( 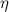= 0,85 Па·с). Эквивалентное обозначение единиц, в которых измеряется коэффициент вязкости: Па·с=кг·м–1·с–1.
Между движущимся телом и средой всегда существуют силы сцепления, так что непосредственно вблизи поверхности тела слой газа (жидкости) полностью задерживается, как бы «прилипая» к нему. Он трется о следующий слой, который слегка отстает от тела. Тот, в свою очередь, испытывает силу трения со стороны еще более удаленного слоя и т.д. Совсем далекие от тела слои можно считать покоящимися. Теоретический расчет внутреннего трения для движения шарика диаметром D приводит к формуле Стокса:
Подставляя формулу Стокса в выражение для силы сопротивления при установившемся движении, находим выражение для установившейся скорости падения шарика в среде:
Видно, что чем легче тело, тем меньше скорость его падения в атмосфере. Полученное уравнение объясняет нам, почему пушинка падает медленнее,чем стальной шарик.
При решении реальных задач, например, вычислении установившейся скорости падения парашютиста при затяжном прыжке, не следует забывать, что сила трения пропорциональна скорости тела лишь для относительно медленного ламинарного встречного потока воздуха. При увеличении скорости тела вокруг него возникают воздушные вихри, слои перемешиваются, движение в какой-то момент становится турбулентным, и сила сопротивления резко возрастает. Внутреннее трение (вязкость) перестает играть сколько бы то ни было заметную роль.
Рис. 9.15 Фотография струи жидкости при переходе от ламинарного течения к турбулентному (число Рейнольдса Re=250)
Возникновение силы сопротивления можно тогда представить себе следующим образом. Пусть тело прошло в среде путь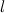 
. При силе сопротивления 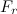на это затрачивается работа
Если площадь поперечного сечения тела равна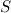 
, то тело «натолкнется» на частицы, занимающие объем 
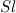. Полная масса частиц в этом объеме равна 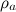· 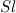Представим, что эти частицы полностью увлекаются телом, приобретая скорость . Тогда их кинетическая энергия становится равной
Эта энергия не появилась ниоткуда: она создана за счет работы внешних сил по преодолению силы сопротивления. Стало быть, A=К, откуда
Мы видим, что теперь сила сопротивления сильнее зависит от скорости движения, становясь пропорциональной ее второй степени (ср. с формулой Стокса). В отличие от сил внутреннего трения ее часто называют силой динамического лобового сопротивления.
Однако предположение о полном увлечении частиц среды движущимся телом оказывается слишком сильным. В реальности любое тело так или иначе обтекается потоком, что уменьшает силу сопротивления. Принято использовать так называемый коэффициент сопротивления C, записывая силу лобового сопротивления в виде:
При турбулентном потоке в некотором интервале скоростей C не зависит от скорости движения тела, но зависит от его формы: скажем, для диска он равен единице, а для шара примерно 0,5.
Подставляя формулу для силы лобового сопротивления в выражение для силы сопротивления при установившемся движении, приходим к иному, нежели ранее полученная формула, выражению для установившейся скорости падения шара (при C = 0,5):
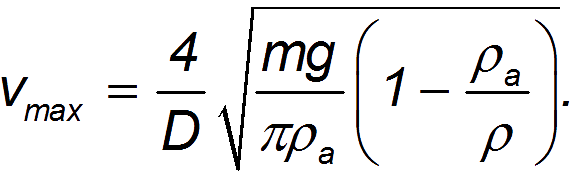
Применяя найденную формулу к движению парашютиста весом 100 кг с поперечным размером парашюта 10 м, находим
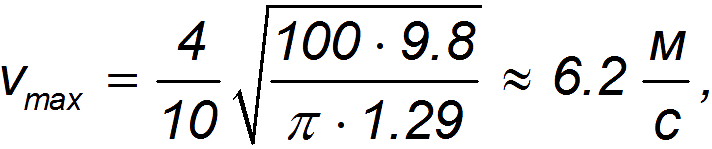
что соответствует скорости приземления при прыжке без парашюта с высоты 2 м. Видно, что для описания движения парашютиста больше подходит формула, соответствующая турбулентному потоку воздуха.
Выражение для силы сопротивления с коэффициентом сопротивления удобно использовать во всем интервале скоростей. Поскольку при малых скоростях режим сопротивления меняется, то коэффициент сопротивления в области ламинарного течения и в переходной области к турбулентному течению будет зависеть от скорости тела. Однако прямая зависимость C от невозможна, поскольку коэффициент сопротивления безразмерен. Значит, он может быть лишь функцией какой-то безразмерной комбинации с участием скорости. Такая комбинация, играющая важную роль в гидро- и аэродинамике, называется числом Рейнольдса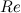 
(см. тему 1.3).
Число Рейнольдса — это параметр, описывающий смену режима при переходе от ламинарного течения к турбулентному. Таким параметром может служить отношение силы лобового сопротивления к силе внутреннего трения. Подставляя в формулу для силы сопротивления выражение для площади поперечного сечения шара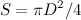 
, убеждаемся, что величина силы лобового сопротивления с точностью до несущественных сейчас числовых факторов определяется выражением
а величина силы внутреннего трения — выражением
Отношение этих двух выражений и есть число Рейнольдса:
Если речь идет не о движении шара, то под D понимается характерный размер системы (скажем, диаметр трубы в задаче о течении жидкости). По самому смыслу числа Рейнольдса ясно, что при его малых значениях доминируют силы внутреннего трения: вязкость велика и мы имеем дело с ламинарным потоком. При больших значениях числа Рейнольдса, наоборот, доминируют силы динамического лобового сопротивления и поток становится турбулентным.
Число Рейнольдса имеет огромное значение при моделировании реальных процессов в меньших (лабораторных) масштабах. Если для двух течений разных размеров числа Рейнольдса одинаковы, то такие течения подобны, и возникающие в них явления могут быть получены одно из другого простым изменением масштаба измерения координат и скоростей. Поэтому, например, на модели самолета или автомобиля в аэродинамической трубе можно предугадать и изучить процессы, которые возникнут в процессе реальной эксплуатации.
Коэффициент сопротивления. Итак, коэффициент сопротивления в формуле для силы сопротивления зависит от числа Рейнольдса:
Эта зависимость имеет сложный характер, показанный (для шара) на рис. 9.16. Теоретически получить эту кривую трудно, и обычно используют зависимости, экспериментально измеренные для данного тела. Однако возможна качественная ее интерпретация.
Рис. 9.16. Зависимость коэффициента сопротивления от числа Рейнолъдса (римскими цифрами показаны области значений Re; которым соответствуют различные режимы течения воздушного потока)
Область I. Здесь число Рейнольдса очень мало (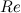 < 1) и течение потока ламинарно. Экспериментальная кривая описывается в этой области функцией
При подстановке этого значения в найденную ранее формулу для силы сопротивления и использовании 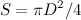и выражения для числа Рейнольдса мы приходим к формуле Стокса. В этой области, как уже говорилось, сопротивление возникает вследствие вязкости среды.
Область II. Здесь число Рейнольдса лежит в интервале 1 < 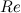< 2·104. Данная область соответствует переходу от ламинарного к турбулентному течению. Экспериментальные данные свидетельствуют, что при увеличении числа Рейнольдса достигается некоторое его критическое значение, после которого стационарное ламинарное течение становится неустойчивым. Разумеется, это критическое значение не универсально и различается для разных типов течений. Но его характерная величина порядка нескольких десятков.
При 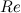лишь слегка больших критического значения появляется нестационарное периодическое движение потока, характеризуемое некоторой частотой. При дальнейшем увеличении 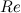периодическое движение усложняется, и в нем появляются новые и новые частоты. Этим частотам соответствуют периодические движения (вихри), пространственные масштабы которых становятся все более мелкими. Движение приобретает более сложный и запутанный характер — развивается турбулентность. В данной области коэффициент сопротивления продолжает падать с ростом 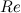, но медленнее. Минимум достигается при 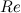= (4–5)·103, вслед за чем С несколько повышается.
Область III. Эта область соответствует развитому турбулентному течению потока вокруг шара, а с этим режимом мы уже встречались выше. Характерные здесь значения числа Рейнольдса лежат в интервале 2·104 < 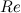< 2·105.
При движении тело оставляет за собой турбулентный след, за пределами которого течение ламинарно. Вихревой турбулентный след легко наблюдать, например, за кормой корабля. Часть поверхности тела непосредственно примыкает к области турбулентного следа, а его передняя часть — к области ламинарного течения. Граница между ними на поверхности тела называется линией отрыва. Физической причиной возникновения силы сопротивления является разность давлений на передней и задней поверхностях тела. Оказывается, что положение линии отрыва определяется свойствами пограничного слоя и не зависит от числа Рейнольдса. Поэтому коэффициент сопротивления примерно постоянен в этом режиме.
Область IV. Однако такой режим обтекания тела не может поддерживаться до сколь угодно больших значений 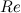. В какой-то момент передний ламинарный пограничный слой турбулизируется, что отодвигает назад линию отрыва. Турбулентный след за телом сужается, что приводит к резкому (в 4–5 раз) падению сопротивления среды. Это явление, названное кризисом сопротивления, происходит в узком интервале значений 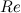= (2–2,5)·105. Строго говоря, приведенные теоретические соображения могут измениться при учете сжимаемости среды (воздуха, в нашем случае). Однако это проявится, как мы уже обсуждали, при скоростях объектов, сравнимых со скоростью звука.
Дополнительная информация
http://ilib.mirror1.mccme.ru/djvu/bib-kvant/kvant_70.djvu — Стасенко А.Л. Физика полета, Библиотечка Квант, выпуск 70 стр. 17–28 — аэродинамические силы, действующие на крыло.
http://d.theupload.info/down/8osiz73swyx22j1icv3641f3xxe8rtdp/butikov_e_i__kondratev_a_s__fizika_dlja_uglublennogo_izuchen.djvu — Е.И. Бутиков, А.С.Кондратьев, Учебное пособие; Кн. 1, Механика, Физматлит, 2001 г. — глава V — движение жидкостей и газов.
Список дополнительных ссылок
http://kvant.mirror1.mccme.ru/pdf/1998/02/kv0298fizfak.pdf — журнал «Квант» — математический маятник на наклонных поверхностях (П. Хаджи, А. Михайленко).
http://kvant.mirror1.mccme.ru/1971/06/strannyj_mayatnik.htm — журнал «Квант» — математический маятник с подвижной точкой подвеса (Н. Минц);
http://edu.ioffe.ru/register/?doc=physica/lect4.ch1.tex — В лекции рассматриваются гармонические колебания, фазовый портрет маятника, адиабатические инварианты.
http://www.plib.ru/library/book/9969.html — Е.И. Бутиков, А.С. Кондратьев, Учебное пособие; Кн. 1, Механика, Физматлит, 2001 г. — стр. 279–295 (§§ 42,43) — описаны затухающие колебания при сухом трении и собственные колебания в разных физических системах.
http://mechanics.h1.ru/ — Механика в школе, определения основных физических величин, решение задач.
http://edu.ioffe.ru/register/?doc=mgivanov — Курс лекций по механике для физико-технической школы (М.Г. Иванов).
http://ilib.mirror1.mccme.ru/djvu/bib-kvant/kvant63.djvu — Асламазов Л.Г., Варламов А.А. Удивительная физика, Библиотечка Квант, выпуск 63, глава 2 — простая физика сложных явлений.
http://schools.keldysh.ru/sch1275/kross/ — Физические кроссворды.
http://www.newsland.ru/News/Detail/id/211926/22 — Обсуждается возможность создания звуковой и оптической «шапки-невидимки».
http://ilib.mirror1.mccme.ru/djvu/bib-kvant/kvant_40.djvu — Хилькевич С.С., Физика вокруг нас, библиотечка Квант, выпуск 40, глава 1, § 5 — как действует на смесь вибрация и что происходит при встряхивании ведра с картошкой.
