ГЛАВА 8. СИЛА УПРУГОСТИ. СИЛА ТРЕНИЯ
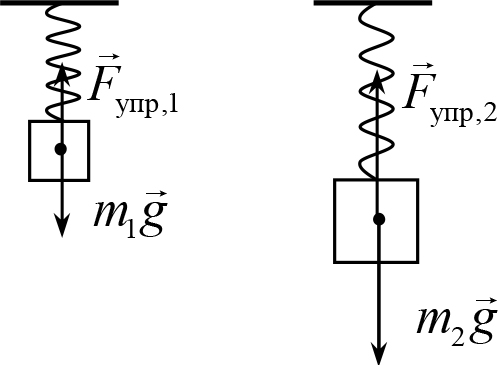
Рис. 8.2
Решая систему уравнений (8.3) относительно неизвестных k и l0, получим
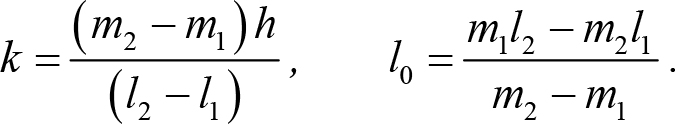
Пример 8.2. Тело массой m, подвешенное на пружине с коэффициентом жесткости k, совершает колебания в вертикальном направлении. Найти удлинение пружины (по сравнению с недеформированным состоянием) в такие моменты времени, когда:
- (а) ускорение тела равно нулю,
- (б) ускорение тела в полтора раза больше ускорения свободного падения и направлено вертикально вниз,
- (в) скорость тела максимальна.
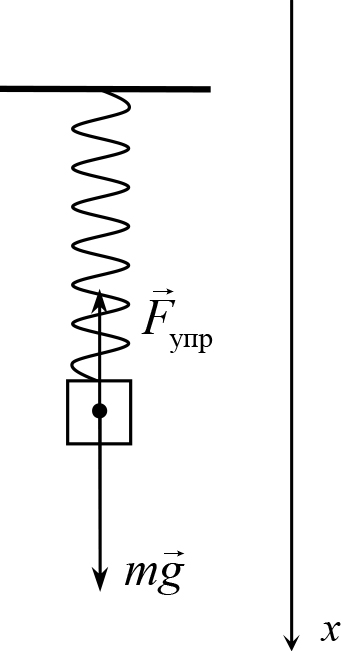
Рис. 8.3
Решение. Когда тело, прикрепленное к пружине, движется, причем так, что деформация пружины изменяется в процессе движения, то на тело действует переменная сила упругости, и, следовательно, мгновенное ускорение тела изменяется в процессе движения. Поэтому движение такого тела является гораздо более сложным, чем равноускоренное. Подробно движение тела на пружине будет исследовано в главе, посвященной гармоническим колебаниям. Здесь найдем только ускорения тела в разные моменты времени.


