ГЛАВА 8. СИЛА УПРУГОСТИ. СИЛА ТРЕНИЯ
(ж) Читателю, заинтересовавшемуся силой трения, мы рекомендуем прочитать главы, посвященные силе трения, в замечательных книгах Р. Лейтона, М. Сэндса и Р. Фейнмана, «Фейнмановские лекции по физике», т. 1 (М.: Мир, 1977), и Л.Г. Асламазова и И.Ш. Слободецкого «Задачи и не только по физике» (М.: Техно-сфера, 2005).
Подведем итоги. Согласно логике Ньютона для всех сил должны существовать независимые от второго закона Ньютона формулы, выражающие эти силы через координаты и (может быть) скорости входящих в задачу тел. Эти выражения, будучи подставленными во второй закон Ньютона, позволяют находить ускорения тел, а затем и законы их движения.
Для рассмотренных в настоящей главе сил упругости и трения такие выражения даются законами Гука и Кулона-Амонтона. Эти формулы вместе со вторым законом Ньютона позволяют решить любую динамическую задачу, в которых участвуют эти силы. При этом нужно помнить о необходимости проводить анализ альтернативы «покой-скольжение», если из условия задачи неясно, движется тело, или нет. Давайте рассмотрим еще два примера.
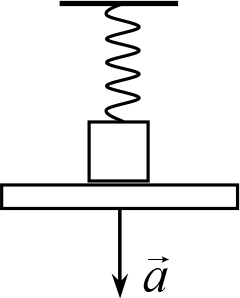
Рис. 8.6
Пример 8.5. На подставке лежит тело, подвешенное к потолку с помощью пружины. В начальный момент пружина не деформирована. Подставку начинают опускать вниз с ускорением ![]() (рис. 8.6). Через какой промежуток Δt тело оторвется от подставки? Коэффициент жесткости пружины k, масса тела m. Куда направлен вектор ускорения тела сразу после того, как оно оторвется от подставки?
(рис. 8.6). Через какой промежуток Δt тело оторвется от подставки? Коэффициент жесткости пружины k, масса тела m. Куда направлен вектор ускорения тела сразу после того, как оно оторвется от подставки?
Решение. В этой задаче есть два не примитивных момента. Первый – это то, что тело до момента отрыва от подставки будет двигаться с постоянным ускорением. Вещь простая, ведь тело движется вместе с подставкой, а она – с постоянным ускорением. И все-таки часто школьники боятся этого простого вывода, поскольку знают, что при движении тела на пружине его ускорение изменяется. Если бы на тело действовала только сила упругости, или сила упругости и какая-то постоянная сила (например, сила тяжести), это было бы правильно.


