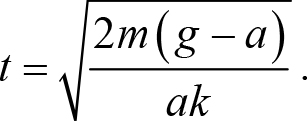ГЛАВА 8. СИЛА УПРУГОСТИ. СИЛА ТРЕНИЯ

Поэтому второй закон Ньютона для тела на подставке в проекциях на ось, направленную вертикально вниз, дает

Из соотношения (8.23) находим силу реакции, действующую на тело со стороны подставки в процессе его движения

где Δx – деформация пружины. Из соотношения (8.24) следует, что сила реакции подставки изменяется в процессе ее движения и становится равной нулю при

Следовательно, при таком растяжении пружины тело оторвется от подставки.

Итак, мы имеем два разных ответа для удлинения пружины, при котором тело оторвется от подставки: (8.22) и (8.25). Ясно, что правильной является формула (8.25), поскольку она получена «честно», без всяких «придумываний». А что же было неправильного в рассуждениях абзаца, предшествующего соотношению (8.22)?

Неправильной была основная идея: отрыв тела от подставки, движущейся с ускорением, произойдет не тогда, когда пружина остановит тело, а тогда, когда сила тяжести и сила упругости не смогут сообщить телу такое же ускорение, как у подставки. Поэтому в момент отрыва ускорение тела не будет равно нулю (как было бы в случае, если отрыв происходил бы при удлинении (8.22)), ускорение тела будет (как и ускорение подставки) направлено вниз, только оно будет меньше ускорения подставки.

Дальнейшая техническая реализация совсем несложна. Так как тело до отрыва от подставки движется равноускоренно и проходит до отрыва расстояние Δx₀ (8.25), то из законов равноускоренного движения легко находим время, прошедшее от начала движения до отрыва