ГЛАВА 9. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА
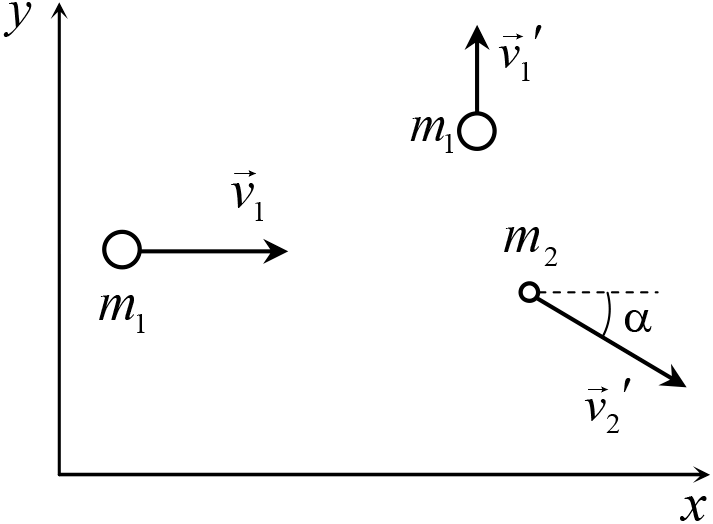
Рис. 9.3
Решение этого уравнения относительно неизвестной скорости второго тела дает
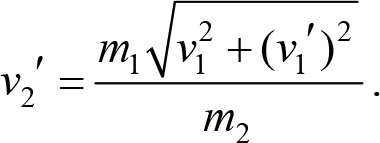
Если перенести слагаемое ![]() во втором уравнении системы (9.7) в левую часть и разделить второе уравнение на первое, получим уравнение относительно тангенса угла
во втором уравнении системы (9.7) в левую часть и разделить второе уравнение на первое, получим уравнение относительно тангенса угла ![]() , решая которое, получим
, решая которое, получим
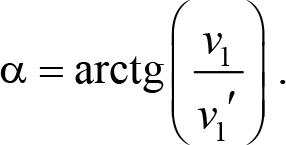
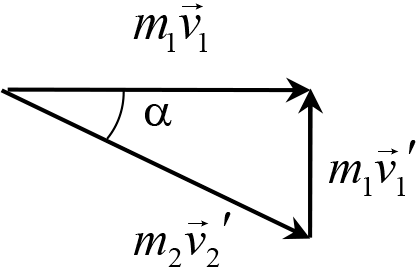
Рис. 9.4
Те же самые результаты можно было получить геометрически с помощью следующих рассуждений. Из закона сохранения импульса следует, что три вектора ![]() ,
, ![]() и
и ![]() образуют треугольник (рис. 9.4), длины сторон которого равны модулям этих векторов, а углы – углам между векторами. Из этого треугольника мгновенно получаются те же формулы для
образуют треугольник (рис. 9.4), длины сторон которого равны модулям этих векторов, а углы – углам между векторами. Из этого треугольника мгновенно получаются те же формулы для ![]() и
и ![]() , что были получены выше с помощью проецирования закона сохранения импульса на координатные оси.
, что были получены выше с помощью проецирования закона сохранения импульса на координатные оси.
Давайте подведем итоги. Закон сохранения импульса утверждает, что импульс замкнутой системы тел не зависит от времени – сохраняется. А поскольку импульс системы тел выражается через импульсы тел системы, закон сохранения импульса можно использовать для нахождения скоростей тел системы. Технически использование закона сохранения импульса сводится к выполнению следующих действий.


