ГЛАВА 9. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА
В результате оказалось, что обе величины при определенных условиях сохраняются, одна из них – это вектор импульса тела, вторая – удвоенная кинетическая энергия.
Закон сохранения импульса позволяет находить скорости тел. Действительно, закон (9.6) утверждает, что скорости тел не могут меняться произвольно: и если известна скорость одного из тел после взаимодействия, то скорость второго в этот момент времени однозначно определяется законом (9.6). Подчеркнем, что закон сохранения импульса является векторным, поэтому связь между значениями скоростей можно установить с помощью геометрического рассмотрения уравнения (9.6) или с помощью его проецирования на оси вспомогательной системы координат. Рассмотрим пример.
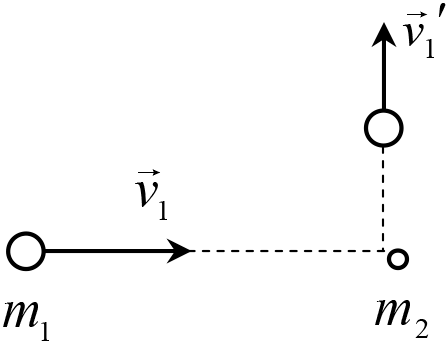
Рис. 9.2
Пример 9.2. Тело массой m1 налетает со скоростью ![]() на неподвижное тело с массой m2 и после удара движется со скоростью
на неподвижное тело с массой m2 и после удара движется со скоростью ![]() в направлении, перпендикулярном первоначальному (рис. 9.2). Определить направление движения и скорость второго тела после удара. Считать, что система тел замкнута.
в направлении, перпендикулярном первоначальному (рис. 9.2). Определить направление движения и скорость второго тела после удара. Считать, что система тел замкнута.
Решение. Поскольку система тел по условию замкнута, для нее справедлив закон сохранения импульса, который при нулевой скорости второго тела до столкновения имеет вид
![]()
где ![]() – скорость второго тела после столкновения. Проецируем закон сохранения импульса на оси, одна из которых (x) направлена вдоль вектора
– скорость второго тела после столкновения. Проецируем закон сохранения импульса на оси, одна из которых (x) направлена вдоль вектора ![]() , вторая (y) – вдоль
, вторая (y) – вдоль ![]() (рис. 9.3). Получаем
(рис. 9.3). Получаем
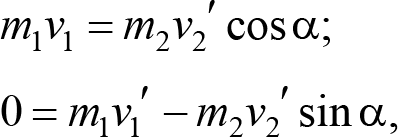
где α — угол между осью x и вектором ![]() (рис. 9.3). Перенося слагаемое
(рис. 9.3). Перенося слагаемое ![]() во втором уравнении системы (9.7) в левую часть, возводя уравнения в квадрат и складывая, получаем уравнение, в которое не входит угол α.
во втором уравнении системы (9.7) в левую часть, возводя уравнения в квадрат и складывая, получаем уравнение, в которое не входит угол α.


