ГЛАВА 11. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ. ЗАКОН СОХРАНЕНИЯ И ИЗМЕНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ
4. И независимо от того, сохраняется или нет механическая энергия, можно использовать теорему об изменении кинетической энергии: разность конечной и начальной кинетической энергии равна работе всех сил (и потенциальных, и непотенциальных), действующих на даннoе тело. Давайте рассмотрим еще один пример.
5. И еще раз напоминаем, что все энергетические соотношения не являются векторными, не требуют проецирования на координатные оси и т.д. Векторный характер законов механики входит в эти соотношения только через знак работы. Поэтому использование энергетических соотношений технически является достаточно простым.
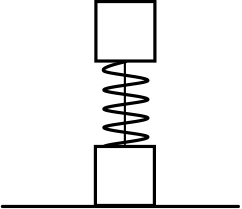
Рис. 11.6
Пример 11.3. Между двумя кубиками массой m находится пружина с коэффициентом жесткости k. В начальный момент пружина сжата на величину Δl по сравнению с недеформированным состоянием, а кубики связаны нитью (рис. 11.6). Нить перерезают. При каких значениях Δl нижний кубик подпрыгнет в процессе дальнейшего движения? Силой сопротивления воздуха пренебречь.
Решение. После перерезания нити пружина начнет разжиматься, поднимая верхний кубик. В этот момент на нижний кубик также действует сила упругости, но направленная вниз, которая вместе с силой тяжести прижимает его к опоре. Если в процессе движения верхнего кубика сжатие пружины сменится растяжением (это зависит от величины первоначального сжатия Δl), то сила упругости, действующая на кубики, изменит направление, нижний кубик она будет уже тянуть вверх, стараясь оторвать его от опоры. Поэтому нижний кубик оторвется от опоры, если в процессе движения верхнего кубика растяжение пружины станет таким, что сила упругости пружины в этот момент будет больше, чем сила тяжести, действующая на нижний кубик. Силу упругости можно найти по закону Гука через удлинение пружины. А как же найти максимальное удлинение пружины? Следует применить к движению верхнего кубика закон сохранения механической энергии или теорему об изменении кинетической энергии при условии, что нижний кубик еще не оторвался от опоры. Продемонстрируем, как работает закон сохранения энергии.
Выбираем начало отсчета потенциальной энергии силы тяжести для верхнего кубика в точке его начального положения.


