ГЛАВА 12. ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ. КИНЕМАТИКА И ДИНАМИКА
Быстрота вращения тела характеризуется угловой скоростью ω, которая определяется как отношение угла поворота тела к тому интервалу времени, за которое этот поворот произошел
С выражением (12.1) связана та же логика определения средней и мгновенной величины, которая связана с определением обычной (в этом контексте говорят линейной скорости): для большого промежутка времени Δt формула (12.1) дает среднюю за этот промежуток угловую скорость тела, в пределе Δt → 0 – мгновенную. Если тело вращается равномерно (а только такое вращательное движение рассматривается в школьном курсе физики), то формула (12.1) дает одинаковые результаты для любых промежутков времени.
Поскольку угловая скорость определяется через углы поворота, скажем два слова о единицах измерения углов. Наиболее распространенными являются градус и радиан. Градус определяется как угол, равный 1/360 полного угла. Очевидно, что это неудачная единица, поскольку число 360 «втиснуто» в задачу измерения углов «насильно», а не возникло в ней самой (почему, например, не 100, или не 420, или вообще не 333?). В результате математика «мстит» за такое насилие над собой появлением множителя π / 180 в ряде формул, который возникает именно из-за плохих единиц измерения углов.
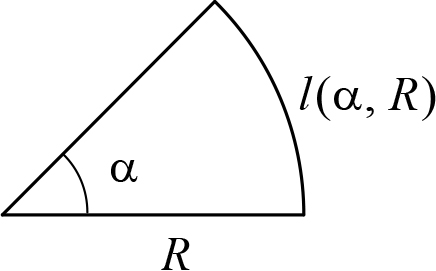
Для углов существует абсолютно естественная мера измерения – радиан, при введении которого используется следующая прозрачная логика. Рассмотрим некоторый угол α и построим сектор некоторого радиуса R, опирающийся на этот угол (рис. 12.1). Длина дуги этого сектора зависит от величины угла и радиуса – l(α, R). Очевидно, зависимость длины дуги от угла – прямо пропорциональная.


