ГЛАВА 23. ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРИЧЕСКИХ ЗАРЯДОВ. ЗАКОН КУЛОНА. ПРИНЦИП СУПЕРПОЗИЦИИ
Сила взаимодействия такого заряда и пластины не зависит от расстояния между ними и определяется соотношением
где величина 
= Q / S имеет смысл заряда единицы площади пластины или поверхностной плотности заряда пластины. Формула (23.8) является приближенной: она справедлива тем лучше, чем меньше расстояние d по сравнению с расстоянием от точечного заряда до краев пластины. Другими словами, заряд должен находиться близко к пластине, но далеко от ее краев. Только такие ситуации и рассматриваются в школьном курсе физики. Часто о них говорят как о возможности пренебречь «краевыми эффектами». Подчеркнем, что формулы (23.7)-(23.8) - результат сложных вычислений для сфер и плоскостей, основанных на принципе суперпозиции.
На основе формул (23.7)-(23.8) можно комбинировать точечные заряды, сферы и плоскости. Такие задачи входят в школьный курс физики, и школьники должны уметь их решать. Рассмотрим два примера.
Пример 23.5. Имеются три концентрических сферы радиусов R, 2R и 3R , заряженные зарядами Q, −2Q и 3Q - соответственно. Точечный заряд q расположен на расстоянии r = 5R / 2 от общего центра сфер (т.е. между второй и третьей сферами). Найти силу, действующую на точечный заряд.
Решение. Согласно принципу суперпозиции каждая сфера оказывает воздействие на точечный заряд независимо от других сфер. Поэтому найдем силы, действующие на него со стороны каждой сферы, сложим полученные векторы.
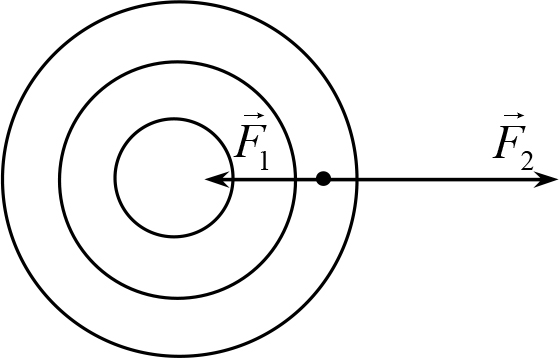
Рис. 23.6
Согласно формуле (23.7) внешняя сфера вообще не действует на точечный заряд (ведь он находится внутри нее)
средняя - дает силу притяжения (считаем, что Q, q > 0 ) величиной
