ГЛАВА 23. ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРИЧЕСКИХ ЗАРЯДОВ. ЗАКОН КУЛОНА. ПРИНЦИП СУПЕРПОЗИЦИИ
Этот метод заключается в том, протяженное заряженное тело мысленно делится на малые части, которые можно считать точечными зарядами, а затем по закону Кулона находятся силы взаимодействия каждой пары точечных частей. Суммарная сила, действующая на одно из тел, есть векторная сумма сил, действующих на каждую его малую часть со стороны малых частей другого тела.
Важно подчеркнуть, что такая процедура не является только «словесной». В математическом анализе разработаны методы выполнения такого суммирования (основы этих методов были разработаны Ньютоном именно при решении задачи о гравитационном взаимодействии неточечных тел). Владение этими методами не входит в программу школьного курса; школьник должен только понимать идею такого суммирования и уметь его выполнить в тех ситуациях, когда суммирование выполняется «словами» с использованием тех или иных соображений симметрии. И, конечно, необходимо помнить, что закон Кулона справедлив только для точечных тел, и не следует применять его при вычислении сил взаимодействия заряженных нитей или плоскостей. Удивительно, но это последнее утверждение крайне тяжело «входит в умы» современных школьников. И, кроме того, есть два неточечных заряженных тела, формулы для которых нужно просто помнить.
Равномерно заряженная сфера. Пусть имеется сфера радиуса R, равномерно заряженная зарядом Q, и точечный заряд q, находящийся на расстоянии r от центра сферы. Можно доказать на основе принципа суперпозиции, что сила взаимодействия точечного заряда и сферы строго равна нулю, если заряд находится внутри сферы, и определяется формулой Кулона (23.1) с тем же самым коэффициентом, если заряд находится снаружи:
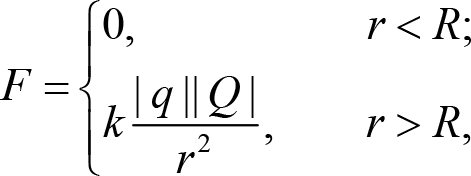
где k - коэффициент закона Кулона. Подчеркнем, что r в формуле (23.7) - расстояние от точечного заряда до центра сферы, а не до ее поверхности.
Равномерно заряженная плоскость. Пусть имеется точечный заряд q, расположенный на расстоянии d от очень большой тонкой пластины (часто говорят - плоскости) площадью S, заряженной зарядом Q.


