ГЛАВА 25. ПРОВОДНИКИ И ДИЭЛЕКТРИКИ В ЭЛЕКТРИЧЕСКОМ ПОЛЕ
Эти рассуждения проще всего понять на конкретном примере, к обсуждению которого мы и переходим.
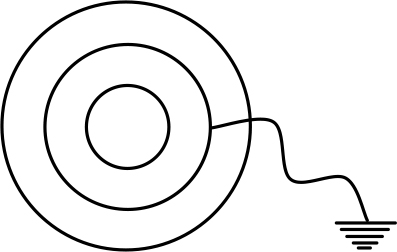
Рис. 25.6
Пример 25.4. Три концентрические сферы с радиусами R, 2R и 3R зарядили зарядами q, 2q и 3q соответственно, а потом среднюю сферу заземлили. Какой заряд протечет по заземляющему проводнику в направлении земли в процессе установления равновесия. Считать, что проводник настолько тонкий, что заряды могут протечь по нему, но не могут на нем оставаться.
Решение. Поскольку внутренняя и внешняя сферы не контактируют с другими телами, их заряды не изменяются. Пусть заряд средней сферы после заземления будет равен Q. Согласно принципу суперпозиции ее потенциал ![]() будет создаваться всеми имеющимися в нашем распоряжении зарядами, а не только ее зарядом. Действительно, потенциал проводника - это потенциал электрического поля в точках, принадлежащих данному проводнику, а поле создается всеми зарядами задачи. Поэтому из формулы потенциала поля сферы (24.17) и принципа суперпозиции имеем для потенциала средней сферы
будет создаваться всеми имеющимися в нашем распоряжении зарядами, а не только ее зарядом. Действительно, потенциал проводника - это потенциал электрического поля в точках, принадлежащих данному проводнику, а поле создается всеми зарядами задачи. Поэтому из формулы потенциала поля сферы (24.17) и принципа суперпозиции имеем для потенциала средней сферы
где ![]() - постоянная закона Кулона. Приравнивая потенциал средней сферы
- постоянная закона Кулона. Приравнивая потенциал средней сферы ![]() (25.3) к нулю, находим ее заряд после заземления
(25.3) к нулю, находим ее заряд после заземления
![]()
Очевидно, заряд, протекший по проводнику в направлении земли, равен убыли заряда средней сферы, т.е. разности ее начального и конечного (именно в такой последовательности) заряда1
![]()
В заключение отметим одно важное обстоятельство. При решении задачи мы пользовались ее сферической симметрией, считая что заряды распределяются по сферам равномерно (только в этом случае для потенциалов поля сферы справедлива формула (24.17).
1 Заряд, протекший в направлении средней сферы, равен приращению ее заряда, т.е. разности ее конечного и начального заряда.


