ГЛАВА 28. МАГНИТНЫЕ ВЗАИМОДЕЙСТВИЯ. МАГНИТНАЯ ИНДУКЦИЯ. СИЛЫ ЛОРЕНЦА И АМПЕРА
Существует лишь несколько простых задач, в которых это суммирование можно сделать без высшей математики. Рассмотрим пример.
Пример 28.1. По кольцу радиуса R течет ток I. Используя закон Био-Савара-Лапласа определить магнитную индукцию в центре кольца, а также в точке, расположенной на оси кольца на расстоянии h от его плоскости.
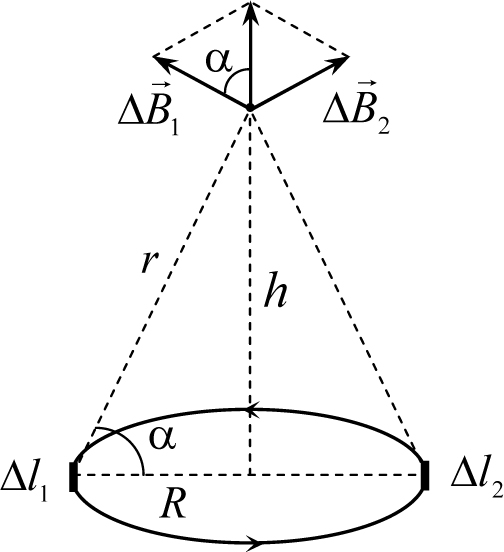
Рис. 28.3
Решение. Процедура нахождения индукции магнитного поля, созданного некоторыми токами, в принципе аналогична нахождению напряженности электрического поля, созданного распределенным электрическим зарядом. Надо мысленно разбить токи на малые элементы (в электростатике разбить заряд на точечные части), по закону Био-Савара-Лапласа найти индукцию магнитного поля создаваемого независимо каждым элементом тока (напряженность электрического поля по закону Кулона в электростатике), сложить получившиеся векторы.
Рассмотрим поле, создаваемое на оси кольца двумя противоположными малыми участками длиной ![]() (на рис. 28.3 эти участки кольца обозначены как
(на рис. 28.3 эти участки кольца обозначены как ![]() и
и ![]() ). По закону Био-Савара-Лапласа находим, что каждый участок кольца создает в точке, находящейся на оси кольца на расстоянии h от его плоскости, магнитное поле с индукцией
). По закону Био-Савара-Лапласа находим, что каждый участок кольца создает в точке, находящейся на оси кольца на расстоянии h от его плоскости, магнитное поле с индукцией
Векторы индукции ![]() и
и ![]() , созданные участками провода
, созданные участками провода ![]() и
и ![]() соответственно, направлены перпендикулярно отрезкам, проведенным из участков кольца
соответственно, направлены перпендикулярно отрезкам, проведенным из участков кольца ![]() и
и ![]() в исследуемую точку (см. рис. 28.3). Поэтому вектор суммы
в исследуемую точку (см. рис. 28.3). Поэтому вектор суммы ![]() +
+ ![]() направлен по оси кольца, а его величина определяется соотношением
направлен по оси кольца, а его величина определяется соотношением ![]() .
.


