ГЛАВА 28. МАГНИТНЫЕ ВЗАИМОДЕЙСТВИЯ. МАГНИТНАЯ ИНДУКЦИЯ. СИЛЫ ЛОРЕНЦА И АМПЕРА
Поскольку все кольцо можно разбить на пары противоположных элементов, то и поле всего кольца будет направлено вдоль его оси, а величина индукции суммарного поля определяется суммой по всем элементам, на которые можно разбить кольцо
Используя формулу (28.2) и учитывая, что 
, а 
, получим
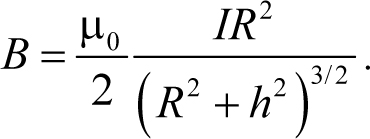
Для индукции в центре кольца ( h = 0 ) эта формула дает
Задача о нахождения магнитного поля кольца на его оси - единственная задача с нахождением индукции магнитного поля, доступная школьникам с точки зрения проведения вычислений. Однако на ее основе можно сделать ряд обобщений на случай более сложных систем.
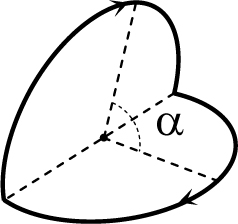
Рис. 28.4
Пример 28.2. Пример 28.2. Во сколько раз изменится индукция магнитного поля в центре кольца с током, если согнуть кольцо по диаметру под углом 
(рис. 28.4)? Ток в кольце при этом не меняется.
Решение. Индукция в центре плоского (не согнутого) кольца определяется соотношением (28.4). Для нахождения поля согнутого кольца воспользуемся законом Био-Савара-Лапласа и принципом суперпозиции. Все участки одного полукольца будут создавать в его центре поле с индукцией, направленной перпендикулярно плоскости полукольца и равной половине индукции (28.4)
где R - радиус кольца; 
- длина элемента. Поэтому ток в каждом полукольце создает в его центре магнитное поле с индукцией
