ГЛАВА 28. МАГНИТНЫЕ ВЗАИМОДЕЙСТВИЯ. МАГНИТНАЯ ИНДУКЦИЯ. СИЛЫ ЛОРЕНЦА И АМПЕРА
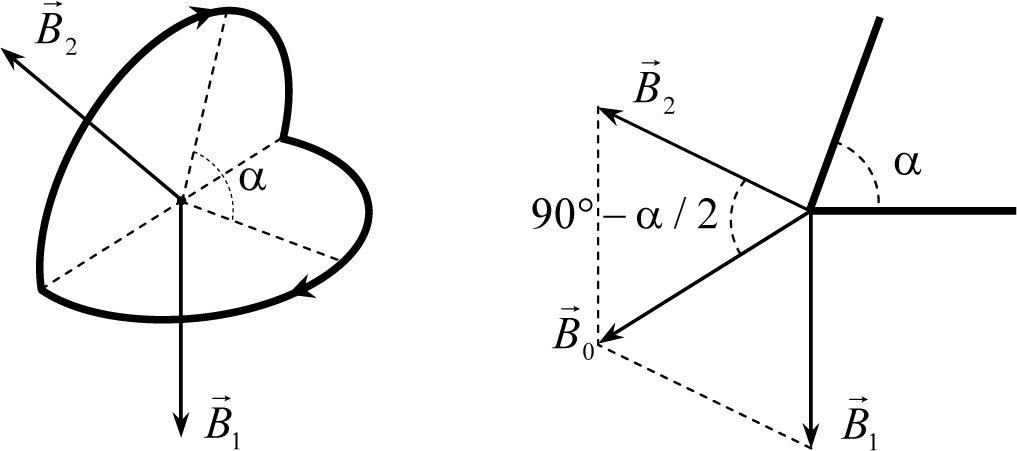
Рис. 28.5
причем векторы индукций магнитного поля каждого полукольца перпендикулярны его плоскости. На рис. 28.5 векторы индукций горизонтального и наклонного полуколец обозначены как 
и 
соответственно; на правом рисунке дан вид полуколец сбоку. Согласно принципу суперпозиции индукция суммарного поля есть векторная сумма векторов и . Поскольку угол между векторами и равен 
, то из (28.6) находим индукцию суммарного магнитного поля в центре полуколец 
Из формул (28.4), (28.7) заключаем, что при сгибании полукольца величина магнитной индукции в его центре уменьшится в
Если полностью согнуть кольцо (
= 0 ), то, как это следует из предыдущей формулы, индукция станет равна нулю. Этот результат очевиден, поскольку при полном сгибании кольца фактически <пропадает> электрический ток - рядом с каждым участком тока будет расположен такой же, участок с противоположно направленным током. Эти два участка создают в каждой точке пространства одинаковые по величине, но противоположно направленные векторы индукции, так, что = 0 .
