ГЛАВА 28. МАГНИТНЫЕ ВЗАИМОДЕЙСТВИЯ. МАГНИТНАЯ ИНДУКЦИЯ. СИЛЫ ЛОРЕНЦА И АМПЕРА
Кроме индукции поля кольца на его оси, существует еще одна задача, для которой индукцию магнитного поля необходимо помнить. Это поле прямого провода с током. Итак, пусть существует бесконечный прямой провод, по которому течет ток I. Тогда этот ток создает магнитное поле, индукция которого на расстоянии r от него, определяется соотношением
Направлен вектор индукции магнитного поля ![]() провода по касательным к окружностям, лежащим в плоскостях, перпендикулярных проводу, центр которых совпадает с проводом. Причем если смотреть на эти окружности в направлении тока в проводе, вектор индукции в каждой точке будет направлен по часовой стрелке. Соотношение (28.8) установлено на основе закона Био-Савара-Лапласа и принципа суперпозиции. Но при ее выводе не обойтись без высшей математики. Поэтому вывод соотношения (28.8) не входит в школьный курс физики, и мы также его не приводим.
провода по касательным к окружностям, лежащим в плоскостях, перпендикулярных проводу, центр которых совпадает с проводом. Причем если смотреть на эти окружности в направлении тока в проводе, вектор индукции в каждой точке будет направлен по часовой стрелке. Соотношение (28.8) установлено на основе закона Био-Савара-Лапласа и принципа суперпозиции. Но при ее выводе не обойтись без высшей математики. Поэтому вывод соотношения (28.8) не входит в школьный курс физики, и мы также его не приводим.
Формула (28.8) позволяет вычислять индукцию магнитного поля, созданного несколькими прямыми проводами, или <кусочками> прямых проводов. Рассмотрим пример.
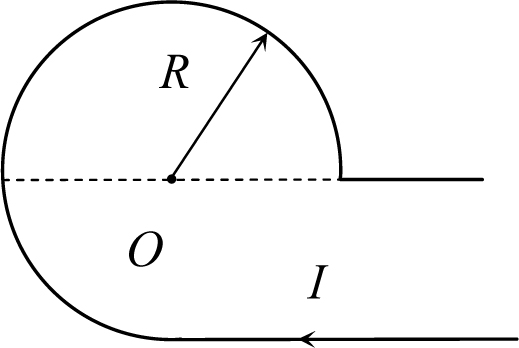
Рис. 28.6
Пример 28.3. Определить индукцию магнитного поля в точке О, если проводник с током I представляет собой два параллельных прямых провода и три четверти кольца радиуса R (рис. 28.6). Точка О - центр кольца.
Решение. Согласно принципу суперпозиции каждый элемент тока создает свое собственное поле независимо от других элементов, а результирующее поле есть векторная сумма этих полей. Но при суммировании поля малых элементов провода мы можем просуммировать сначала по элементам одного прямого провода, затем второго, а затем элементам, входящим в состав кусочка кольца. Поэтому индукция магнитного поля нашего провода представляет собой сумму индукций, создаваемых в любой точке двумя прямыми проводами и проводом, представляющим собой три четверти кольца.


