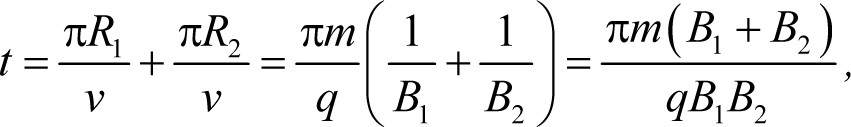ГЛАВА 28. МАГНИТНЫЕ ВЗАИМОДЕЙСТВИЯ. МАГНИТНАЯ ИНДУКЦИЯ. СИЛЫ ЛОРЕНЦА И АМПЕРА
Фактически главное, что нужно запомнить: как бы не двигалась частица, величина ее скорости не изменяется, возможны три траектории движения частицы в однородном магнитном поле. Это либо прямая, либо окружность, либо их комбинация - спираль, которую можно считать <окружностью, непрерывно сдвигаемой в перпендикулярном направлении>. И еще нужно помнить идею метода анализа параметров этой траектории - второй закон Ньютона для частицы и выражение (28.11) для силы, действующей со стороны поля на частицу. В связи с популярностью задач о движении частицы в магнитном поле у составителей заданий ЕГЭ по физике рассмотрим еще один пример.
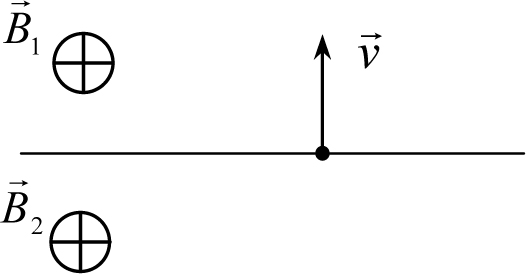
Рис. 28.11
Пример 28.5. В двух полупространствах созданы однородные магнитные поля с индукциями ![]() и
и ![]() , векторы которых параллельны друг другу и границе между полупространствами. В начальный момент времени частица находится на границе раздела полей и имеет скорость v , направленную перпендикулярно границе раздела (рис. 28.11). Найти среднюю скорость перемещения частицы вдоль границы между полупространствами за большое время.
, векторы которых параллельны друг другу и границе между полупространствами. В начальный момент времени частица находится на границе раздела полей и имеет скорость v , направленную перпендикулярно границе раздела (рис. 28.11). Найти среднюю скорость перемещения частицы вдоль границы между полупространствами за большое время.
Решение. Согласно формуле (28.12) в первой области частица будет двигаться по полуокружности радиуса
![]()
во второй
![]()
причем эти полуокружности будут расположены так, как показано на рисунке, который нарисован в предположении, что B2 > B1 и q< > 0. Так как величина скорости частицы не изменяется, то она совершает полный оборот (то есть проходит обе полуокружности) за следующий промежуток времени