ГЛАВА 33. СВЕТОВЫЕ ЛУЧИ. ГЕОМЕТРИЧЕСКАЯ ОПТИКА. ЗАКОНЫ РАСПРОСТРАНЕНИЯ, ОТРАЖЕНИЯ И ПРЕЛОМЛЕНИЯ СВЕТА
Решение. Тень от сваи на дне водоема расположена между основанием сваи и точкой падения на дно луча, проходящего над верхней точкой сваи. Эту тень удобно представить как сумму двух участков — от основания сваи до проекции на дно точки входа
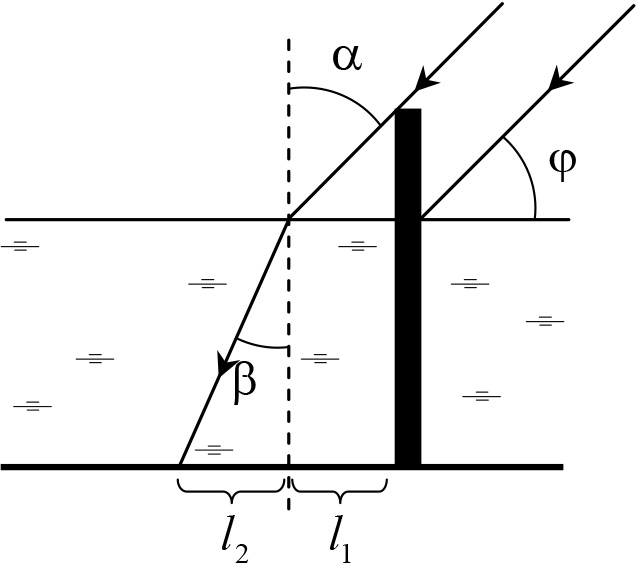
Рис. 33.9
в воду указанного луча l1 и от этой точки до точки падения этого луча на дно l2 (рис. 33.9). Учитывая, что глубина водоема a а высота выступающей над водой части сваи b, получим для длины тени
![]()
где β — угол преломления луча. Поскольку угол падения этого луча α = π/2 – φ, получим из закона преломления
![]()
Выражая тангенс угла β через его синус, найдем
![]()
Пример 33.5. Световой луч падает из воздуха на боковую грань стеклянной призмы под углом β = 45°. Угол между боковыми гранями призмы равен α = 30°. Показатель преломления воздуха равен I, а стекла n = 1,41. Определите угол отклонения луча от первоначального направления распространения.
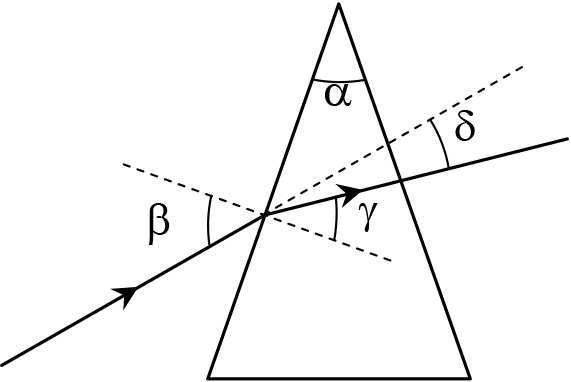
Рис. 33.10
Решение. Рассмотрим сначала преломление луча на первой поверхности. Из закона преломления находим угол преломления луча на первой поверхности
![]()
Это значит, что угол между лучом и перпендикуляром к грани призмы равен приблизительно 30°, а угол между лучом и гранью призмы — равен 60°.


