ГЛАВА 5. ДВИЖЕНИЕ ПОД УГЛОМ К ГОРИЗОНТУ
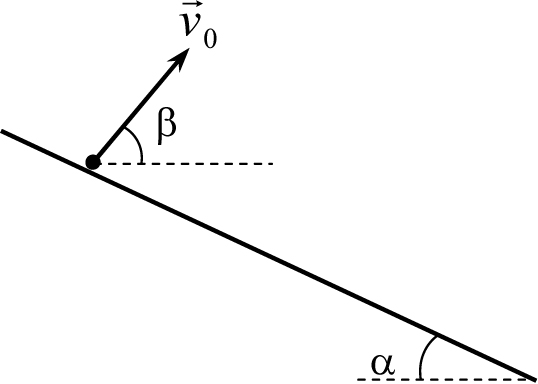
Рис. 5.6
Решение. Поскольку тело движется равноускоренно, зависимости его радиус-вектора ![]() (t) и скорости
(t) и скорости ![]() (t) от времени определяются уравнениями (5.1). Выбираем систему координат так, как показано на рис. 5.7, и проецируем векторные уравнения (5.1) на оси координат. Поскольку угол между вектором
(t) от времени определяются уравнениями (5.1). Выбираем систему координат так, как показано на рис. 5.7, и проецируем векторные уравнения (5.1) на оси координат. Поскольку угол между вектором ![]() 0 и осью x равен α + β (рис. 5.7), то v0,x = v0cos(α + β), v0,y = v0sin(α + β). Угол между вектором
0 и осью x равен α + β (рис. 5.7), то v0,x = v0cos(α + β), v0,y = v0sin(α + β). Угол между вектором ![]() и осью x равен π / 2 − α (см. вставку справа вверху на рис. 5.7), поэтому gx = gsin α, gy = gcos α. Отсюда получаем проекции векторных уравнений на координатные оси
и осью x равен π / 2 − α (см. вставку справа вверху на рис. 5.7), поэтому gx = gsin α, gy = gcos α. Отсюда получаем проекции векторных уравнений на координатные оси
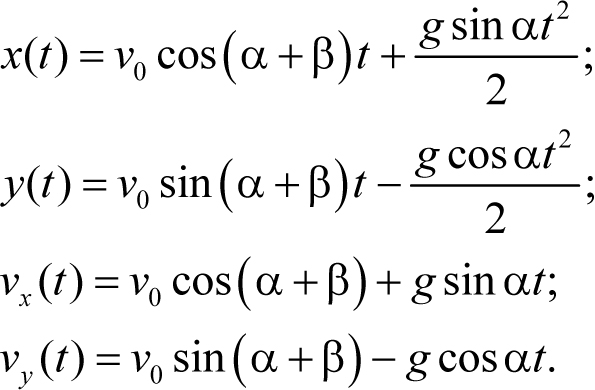
Из уравнений (5.11) следует, что в рассматриваемой системе координат движение не разделилось на равномерное вдоль оси x и равноускоренное вдоль оси y. Однако увеличение сложности уравнений в такой системе координат компенсируется существенно более простыми условиями, определяющими исследуемые точки. Действительно, в тот момент, когда расстояние между телом и плоскостью максимально, вектор скорости тела параллелен плоскости. Поэтому проекция скорости тела в этот момент на ось, перпендикулярную плоскости, равна нулю. Следовательно, подстановка неизвестного времени t1, прошедшего от броска тела до того момента, когда расстояние между ним и плоскостью максимально, в последнее из уравнений (5.11) обращает его левую часть в нуль
![]()


