ГЛАВА 5. ДВИЖЕНИЕ ПОД УГЛОМ К ГОРИЗОНТУ
Применяем уравнения (5.10) к точке падения, т.е. подставляем в них время падения тела на землю τ (оно нам пока неизвестно). Поскольку в момент падения y-координата тела равна h, первое из уравнений (5.10) дает для точки падения
![]()
Откуда находим время падения ![]() . Теперь можно найти и остальные характеристики точки падения. Подставляя время τ в первое из уравнений (5.10), находим x-координату точки падения, которая при нашем выборе системы координат равна искомому расстоянию от основания башни до точки падения
. Теперь можно найти и остальные характеристики точки падения. Подставляя время τ в первое из уравнений (5.10), находим x-координату точки падения, которая при нашем выборе системы координат равна искомому расстоянию от основания башни до точки падения
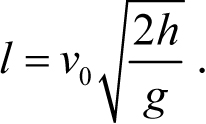
Из последнего уравнения (5.10) находим проекцию вектора скорости тела на ось x в момент падения
![]()
а затем по теореме Пифагора величину конечной скорости
![]()
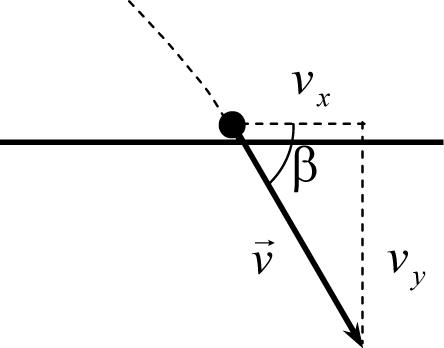
Рис. 5.5
Угол подлета тела к земле – это угол между поверхностью земли и вектором скорости. Из рис. 5.5 находим
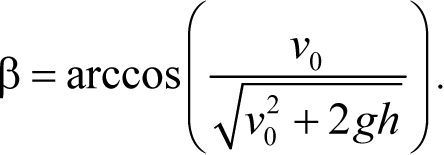
Существует группа задач, в которых рассматривается равноускоренное движение тела около наклонной плоскости, а не возле горизонтальной поверхности. В этом случае, как правило, удобнее проецировать уравнения движения на оси, направленные вдоль плоскости и перпендикулярно к ней, поскольку усложнение уравнений компенсируется более простым их применением к различным точкам траектории. Рассмотрим такую задачу.
Пример 5.4. Тело, находящееся на наклонной плоскости с углом наклона α, бросили под углом β к горизонту с начальной скоростью v0 (рис. 5.6).


