ГЛАВА 5. ДВИЖЕНИЕ ПОД УГЛОМ К ГОРИЗОНТУ
Эти законы позволяют: (а) находить координаты и проекции скорости тела, совершающего криволинейное равноускоренное движение, в любые моменты времени, (б) решать обратную задачу - то есть находить те моменты времени, когда тело имеет те или иные значения координат или проекций скорости.
Технически использование законов движения осуществляется так. Во-первых, необходимо выбрать систему координат, относительно которой задается радиус-вектор тела, и спроецировать уравнения движения на оси этой системы. При нахождении проекций начальной скорости и ускорения необходимо следить за знаками; возможно также появление в уравнениях для проекций тригонометрических функций.
Для правильного использования уравнений движения важно понимать, что время в этих уравнениях – переменная величина, и потому подстановка любого значения в качестве времени t позволяет найти координаты и проекции скорости в этот момент. Рассмотрим еще два примера.
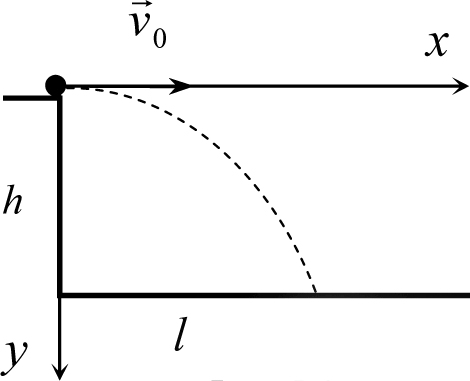
Рис. 5.4
Пример 5.3. Тело брошено горизонтально с начальной скоростью v0 с башни высотой h. На каком расстоянии l от основания башни тело упадет на землю? Какую скорость будет иметь перед самым падением? Под каким углом тело подлетит к земле?
Решение. Проецируем законы движения (5.1) на горизонтальную и вертикальную оси (рис. 5.4) и получаем зависимости координат тела и проекций скорости на оси координат от времени. Имеем
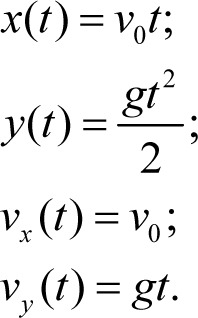
Величина t в уравнениях (5.10) – переменная. Это значит, что подстановка любого значения времени позволяет найти координаты тела и проекции его скорости на оси в этот момент времени.


