ГЛАВА 5. ДВИЖЕНИЕ ПОД УГЛОМ К ГОРИЗОНТУ

Поскольку в нашей системе координат y-координата тела в момент падения на плоскость равна нулю, из второго уравнения (5.11) получаем

Отсюда находим

Полное время движения оказалось вдвое бóльшим времени движения до той точки траектории тела, которая находится на максимальном расстоянии от плоскости. Причем здесь этот вывод совсем неочевиден (как в случае, когда тело бросают около горизонтальной поверхности), ведь траектория тела несимметрична относительно этой точки.

Подставляя время t₂ в уравнение для x-координаты тела, найдем дальность полета

Используя далее формулу сложения тригонометрических функций для выражения в квадратных скобках в числителе, получим

Чтобы исследовать эту величину на максимум как функцию угла β, преобразуем это выражение так, чтобы угол β входил в аргумент только одной тригонометрической функции. Используя тригонометрическую формулу

получаем

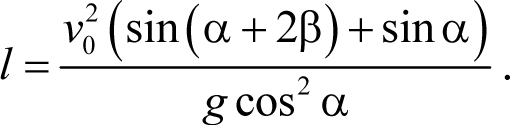
Из этой формулы следует, что дальность полета тела вдоль плоскости как функция угла β максимальна, если аргумент первого синуса в скобках равен π / 2.