ГЛАВА 6. ГРАФИЧЕСКОЕ ОПИСАНИЕ ДВИЖЕНИЯ
Рассмотрим теперь сам момент удара. Пусть время удара (которое по условию очень мало) равно Δt. Тогда проекция среднего ускорения тела за все время удара на ось x равна отношению изменения проекции скорости за время удара к времени удара, то есть
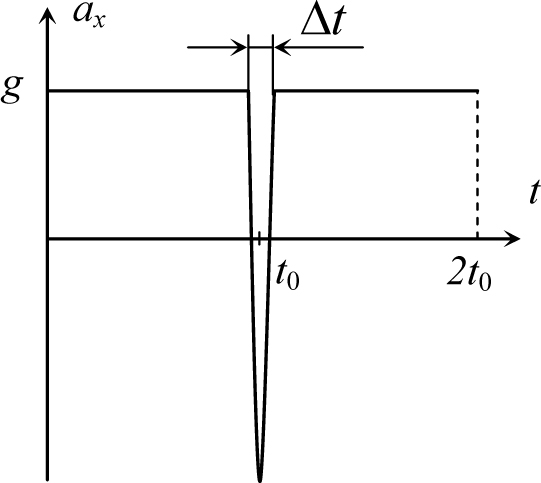
Рис. 6.14
Из выражения (6.10) следует, что в момент удара тела о землю проекция его ускорения на ось x отрицательна, то есть вектор ускорения тела в этот момент направлен вверх, а его величина бесконечно возрастает при Δt → 0 (так как числитель соотношения (6.10) не стремится к нулю при стремлении к нулю знаменателя). Примерная зависимость проекции ускорения на ось x от времени для конечного времени удара Δt приведена на рис. 6.14, причем при уменьшении времени удара минимум на этом рисунке будет становиться «ýже» и «ниже». Именно с такой особенностью поведения ускорения тела связано необычное поведение зависимостей координаты и скорости тела от времени в момент удара. Действительно
Действительно, при доказательстве отсутствия изломов у зависимости координаты от времени и разрывов у скорости в рассмотренных выше примерах предполагалось, что в природе отсутствуют бесконечно большие силы. Таких сил, действительно, не существует. Однако в этой задаче ускорение (и, следовательно, вызывающая его сила взаимодействия тела с поверхностью) становится бесконечно большими в предположении, что время контакта тела с землей Δt → 0. Поэтому предположение о том, что время удара бесконечно мало, является приближенным и представляет собой определенную модель реального взаимодействия. Таким образом, излом на графике координаты и разрыв на графике скорости являются следствием модельного предположения о бесконечной малости времени удара.


