Лемма о вложенных отрезках. Отображения множеств

Лемма

Если последовательность отрезков [a_n; b_n], вложенных друг в друга, т. е. ∀ n[a_n; b_n] [a_n+1; b_n+1] , то существует число c ∈ R, для которого c ∈ [a_n; b_n], ∀ n

Доказательство

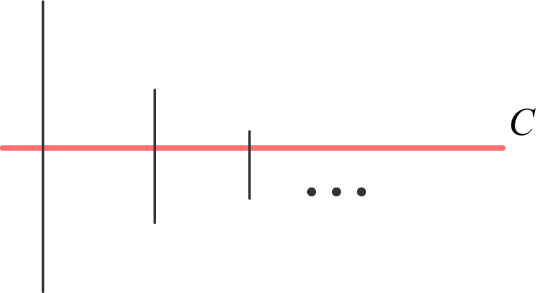
Y — множество левых концов отрезков, Z — множество правых концов. По аксиоме 5 о полноте существует
c ∈ R: a_n ≤ c ≤ b_m для любых n и m. В частности при m = n.