Исследование стационарной точки

Пусть функция f(x) непрерывна в интервале (a − δ; a + δ) и дифференцируема в нём всюду, кроме быть может точки
x = a.

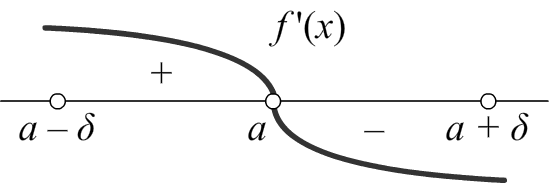
1) Если при переходе через точку x = a производная меняет свой знак с плюса на минус, то точка x = a является точкой максимума.

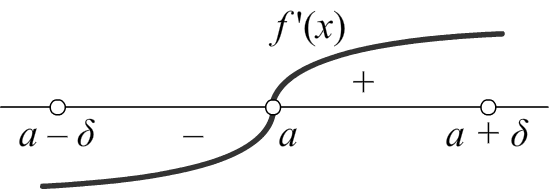
2) Если при переходе через точку x = a производная меняет свой знак с минуса на плюс, то точка x = a является точкой минимума.

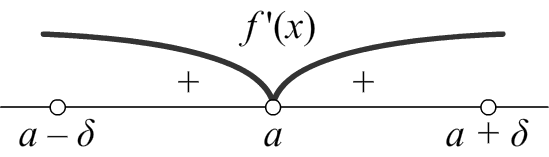
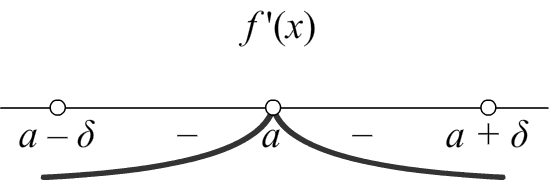
3) Если при переходе через точку x = a производная не меняет знак, то точка x = a точкой экстремума не является.