Исследование стационарной точки
Пример
Исследовать на экстремумы функцию y = x(x − 1)2(x − 2)3
y′ = (x − 1)2(x − 2)3 + 2x(x − 1)(x − 2)3 + 3x(x − 1)2(x − 2)2 =
= (x − 1)(x − 2)2[(x − 1)(x − 2) + 2x(x − 2) + 3x(x − 1)] =
= (x − 1)(x − 2)2[(x2 − 3x + 2) + (2x2 − 4x) + (3x2 − 3x)] =
= (x − 1)(x − 2)2[6x2 − 10x +2] =
= 2(x − 1)(x − 2)2(3x2 − 5x +1)
|
x = x = 1 — максимум x = x = 2 — нет экстремума |



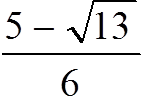 — минимум
— минимум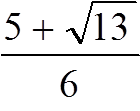 — минимум
— минимум
