Исследование стационарной точки
Пусть функция f(x) дифференцируема в интервале (a − δ; a + δ) и существует f ″(a).
Пусть также f ′(a) = 0, а f ″(a) ≠ 0.
Если f ″(a) < 0, то x = a является точкой строгого максимума f(x).
Если f ″(a) > 0, то x = a является точкой строгого минимума f(x).
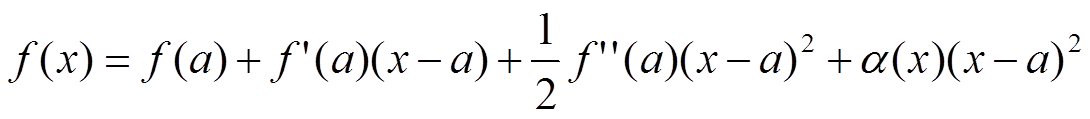
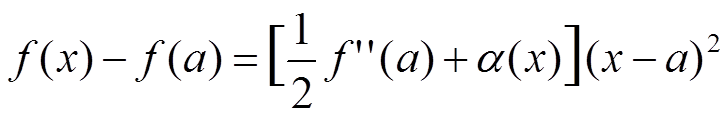
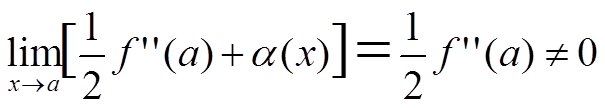
В некоторой окрестности (a − δ1; a + δ1) точки x = a
Sign(f(x) − f(a)) = Signf ″(a)



