Исследование стационарной точки
Пусть функция f(x) имеет n − 1 производную в интервале (a − δ; a + δ) и существует f (n)(a). Пусть также
f′(a) = f ″(a) = ... = f (n−1)(a) = 0, f (n)(a) ≠ 0.
Тогда если
(1) n = 2k + 1 x = a не является точкой экстремума
(2) n = 2k f (n)(a) < 0 x = a является точкой максимума
f (n)(a) > 0 x = a является точкой минимума
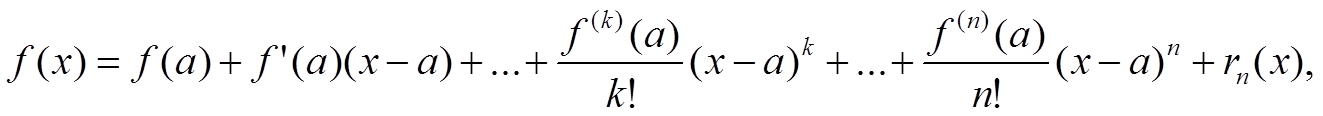
![]()
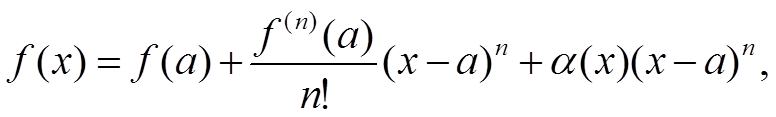
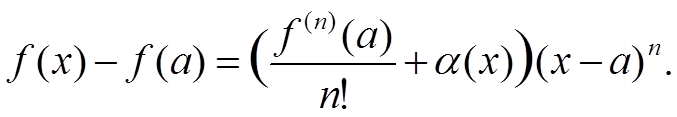
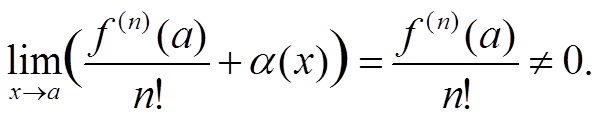
В некоторой окрестности (a − δ1; a + δ1) точки x = a
Sign(f(x) − f(a)) = Sign(f (n)(a)(x − a)(n))



