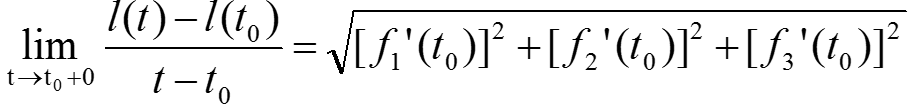Длина кривой

Теорема

Для любой гладкой кривой

Доказательство

Пусть t > t₀, тогда по теореме об аддитивности длины

l(t) − l(t₀) = |∪ M(t₀)M(t)|

Согласно предыдущей теореме для отрезка [t₀; t]

m_i = |f_i′(ξ_i)|, t₀ ≤ ξ_i ≤ t, 1 ≤ i ≤ 3

M_i = |f_i′(η_i)|, t₀ ≤ η_i ≤ t, 1 ≤ i ≤ 3