Определение комплексных чисел и действия с ними в алгебраической форме
Умножение комплексного числа z = (a; b) на вещественное число t определим как tz = (ta; tb).
Тогда z = (a; b) = а(1; 0) + b(0; 1) = а + bi.
Эта форма записи комплексного числа называется алгебраической. Сложение чисел в алгебраической форме происходит естественным путём z1 = a1 + b1i, z2 = a2 + b2i → z1 + z2 = (a1 + a2) + (b1 + b2)i.
Равенство 1 · i = i означает, что умножение единицы на мнимую единицу приводит к повороту единицы на 90°. Сохраним это свойство мнимой единицы для всех комплексных чисел.
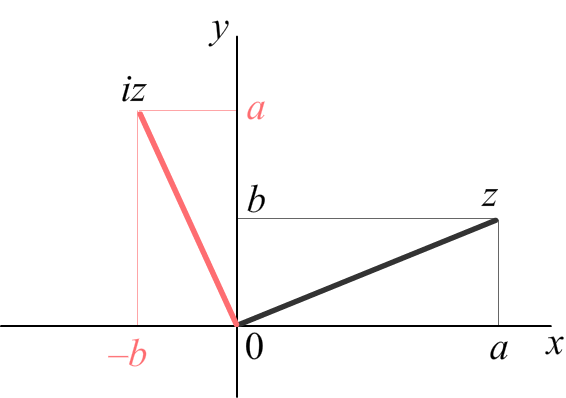
Умножение комплексного числа z = (a; b) на мнимую единицу i определим так, чтобы iz = (−b; a), т. е. вектор на плоскости с координатами (a; b) повернется на 90° против часовой стрелки, не меняя своей длины. |
|