Теорема о переходе к пределу в неравенствах. Теорема о промежуточной функции

Теорема 4

Функции y = f(x), y = g(x) такие, что

1) f(x) ≤ g(x) ∀x ∈ U_θ(a)

2) Тогда A ≤ B.

Доказательство

Противное: A > B.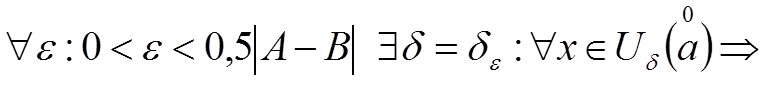

противоречие с 1)

Теорема 5. О знаке функции в окрестности точки

Функция y = f(x), такая, что Тогда существует δ > 0, для которой f(x) > 0 ∀x ∈ _δ(a).

Доказательство

∀ ε < 0,5 A ∃ δ > 0: f(x) > A − ε > 0, ∀x ∈_δ(a)

7/20